7.6.3. Прямые многократные измерения

При статистической обработке группы результатов наблюдений следует выполнить следующие операции:

• исключить известные систематические погрешности из результатов наблюдений;
• вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;
• вычислить оценку среднего квадратического отклонения результата наблюдения (единичного);
• вычислить оценку среднего квадратического отклонения результата измерения (всей серии измерений);
• проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению;
• вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения;
• вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения;
• вычислить доверительные границы погрешности результата измерения.

Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости 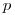от 10 до 2%. Значения уровней значимости должны быть указаны в конкретной методике выполнения измерений ().

Для определения доверительных границ погрешности результата измерения доверительную вероятность 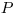принимают равной 0,95. Если измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности 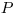= 0,95, допускается указывать границы для доверительной вероятности 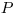= 0,99. В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается принимать еще более высокую вероятность.

За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения систематических погрешностей. Кроме того, из ряда результатов наблюдений необходимо исключить результаты, содержащие грубые погрешности. Способы обнаружения грубых погрешностей должны быть указаны в методике выполнения измерений.

Оценку среднего квадратического отклонения результатов однократный наблюдений 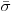вычисляют по формуле

(7.70),

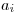где – i-й результат наблюдения; 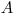— результат измерения (среднее арифметическое исправленных результатов наблюдений); 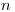— число результатов наблюдений.

Оценку среднего квадратического отклонения результата измерения находят по формуле

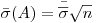(7.71).

Доверительные границы случайной погрешности результата измерения устанавливают обычно для результатов наблюдений, принадлежащих нормальному распределению. Если это условие не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.

При числе результатов наблюдений 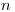> 50 для проверки принадлежности их к нормальному распределению предпочтительным является один из критериев: Пирсона или Мизеса-Смирнова.

При числе результатов наблюдений 50 > 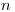> 15 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий.

При числе результатов наблюдений 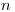< 15 принадлежность их к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности результата измерения по данной методике возможно лишь в случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.

Доверительные границы (без учета знака) случайной погрешности результата измерения находят по формуле

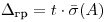(7.72),

где 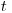— коэффициент Стъюдента, выбираемый из таблиц в зависимости от доверительной вероятности 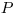и числа результатов наблюдений .

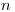Неисключенная систематическая погрешность результата образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности метода, средств измерений и т.д. В качестве границ составляющих неисключенной систематической погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.

При суммировании составляющих неисключенной систематической погрешности результата измерения неисключенные систематические погрешности средств измерений каждого типа и погрешности поправок рассматривают как случайные величины. При отсутствии данных о виде распределения случайных величин их распределения принимают за равномерные.

Границы неисключенной систематической погрешности 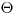результата измерения вычисляют при их равномерном распределении по формуле

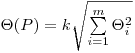(7.73),

где 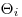— граница i-й неисключенной систематической погрешности; 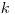— коэффициент, определяемый принятой доверительной вероятностью.

Границы погрешности результата измерения вычисляют следующим образом.

1. Если 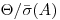< 0,8, неисключенными систематическими погрешностями до сравнению со случайными пренебрегают; и принимают, что граница погрешности результата .

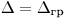Если 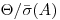> 8, случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что граница погрешности результата .

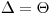2. Если приведенные выше неравенства не выполняются, границу погрешности результата измерения находят путем построения композиции распределения случайных и неисключенных, систематических погрешностей, рассматриваемых как случайные величины. Если доверительные границы случайных погрешностей найдены, границы погрешности результата измерения 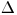(без учета знака) можно вычислить по формуле

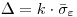(7.74),

где 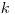— коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешности; 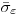— оценка суммарного среднего квадратического отклонения результата измерения.

Оценку суммарного среднего квадратического отклонения результата измерения вычисляют по формуле

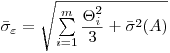(7.75).

Коэффициент 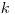вычисляют по эмпирической формуле

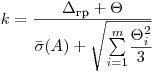(7.76).

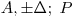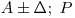Форма представления результата измерения должна соответствовать требованиям МИ 1317-86. При симметричной доверительной погрешности результат измерения представляют в форме: или , где 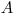— результат измерения. Числовое значение результата измерения должно заканчиваться цифрой того же разряда, что и значение погрешности .

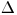При отсутствии данных о виде функций распределений составляющих погрешности результата измерения и необходимости дальнейшей обработки результатов или анализа погрешностей, результат измерения представляют в форме 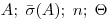.