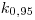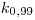7.6.2. Прямые однократные измерения
За результат однократного измерения 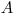 принимают значение физической величины, полученное при отдельном измерении.
принимают значение физической величины, полученное при отдельном измерении.
Составляющие погрешности результата измерения должны быть известны до проведения измерений. Предполагается, что известные систематические погрешности исключены. Однократные измерения имеют место в случае производственной необходимости (разрушение образца, невозможность повторения измерения, экономическая целесообразность и т.д.).
Случайные погрешности считают пренебрежимо малыми по сравнению с неисключенными систематическими, если
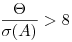 (7.61),
(7.61), где 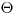 — граница неисключенных систематических погрешностей результата измерения;
— граница неисключенных систематических погрешностей результата измерения; 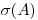 – среднее квадратическое отклонение случайных погрешностей результата измерения.
– среднее квадратическое отклонение случайных погрешностей результата измерения.
Однократные измерения проводятся в тех случаях, когда случайные погрешности существенны, но доверительная граница погрешности результата измерзши не превышает допускаемой погрешности измерений.
Для определения доверительных границ погрешности результата измерения принимают вероятность, равную 0,95. В особых случаях, например, при измерениях, которые нельзя повторить, допускается указывать доверительные границы для более высоких вероятностей.
Погрешность результата измерения (характеристики погрешности и их статистические оценки) выражается числом, содержащим не более двух значащих цифр. Две значащее цифры следует сохранять, если первые две цифры неокругленого числового значения составляют число менее 25·10n. Б этом случае третий разряд (не указываемый младший) округляется в большую сторону (например, 0,151 = 0,16). Одну значащую цифру следует сохранять, если число больше или равно 25·10n. В этом случае округление производят в большую сторону, если цифра последующего неуказанного младшего разряда равна или больше пяти, или в меньшую сторону, если эта цифра меньше пяти.
Составляющие погрешности результата однократного измерения — это погрешности средств измерений, метода и оператора. Эти погрешности могут состоять из неисключенных систематических и случайных погрешностей. Неисключенные систематические погрешности могут быть выражены либо в виде границ 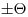 , либо в виде доверительных границ
, либо в виде доверительных границ 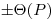 . (В данном разделе для обозначения доверительной вероятности используется буквенное обозначение
. (В данном разделе для обозначения доверительной вероятности используется буквенное обозначение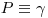 ). Случайные погрешности могут быть представлены средним квадратическим отклонением s или доверительными границами
). Случайные погрешности могут быть представлены средним квадратическим отклонением s или доверительными границами 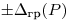 .
.
Погрешности средств измерении определяют по метрологическим характеристикам, которые указаны в нормативно-технической документации, и в соответствии с РД 50-453-84. Погрешности метода ж оператора должны быть определены в нормативно-техническом документе на конкретную методику выполнения измерений.
Оценивание систематической погрешности результата измерения. Если неисключенная систематическая погрешность имела место только у одной из составляющих (погрешности средства измерении, или метода, или оператора), неисключенную систематическую погрешность результата выражают границами этой погрешности.
Доверительные границу неисключенной систематической погрешности результата измерения определяются следующим образом.
При наличии нескольких неисключенных систематических погрешностей, заданных своими границами 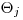 используют формулу
используют формулу
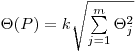 (7.62),
(7.62), где 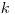 — поправочный коэффициент, определяемый принятой доверительной вероятностью и числом
— поправочный коэффициент, определяемый принятой доверительной вероятностью и числом 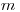 составляющих
составляющих 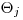 . При доверительной вероятности
. При доверительной вероятности 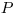 = 0,90 поправочный коэффициент
= 0,90 поправочный коэффициент 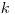 принимают равным 0,95; при доверительной вероятности
принимают равным 0,95; при доверительной вероятности 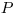 = 0,95
= 0,95 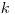 = 1,1. При доверительной вероятности
= 1,1. При доверительной вероятности 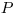 = 0,99 поправочный коэффициент принимают равным 1,45, если число суммируемых составляющих
= 0,99 поправочный коэффициент принимают равным 1,45, если число суммируемых составляющих 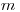 > 4. Если число составляющих
> 4. Если число составляющих 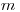 = 4, поправочный коэффициент
= 4, поправочный коэффициент 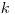 = 1,4; при
= 1,4; при 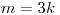 = 1,3; при
= 1,3; при 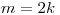 = 1,2.
= 1,2.
При наличии нескольких неисключенных систематических погрешностей, заданных доверительными границами 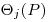 рассчитанными по предыдущей формуле, доверительную границу неисключекной систематической погрешности результата однократного измерения вычисляют по формуле
рассчитанными по предыдущей формуле, доверительную границу неисключекной систематической погрешности результата однократного измерения вычисляют по формуле
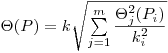 (7.63),
(7.63), где 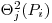 – доверительная граница j-й неисключенной систематической погрешности, соответствующая доверительной вероятности
– доверительная граница j-й неисключенной систематической погрешности, соответствующая доверительной вероятности 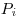 ;
; 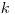 и
и 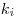 – коэффициенты, соответствующие доверительной вероятности
– коэффициенты, соответствующие доверительной вероятности 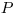 и
и 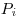 соответственно, значения которых определяют в соответствии с принципами изложенными выше.
соответственно, значения которых определяют в соответствии с принципами изложенными выше.
Оценивание случайной погрешности результата измерения производится следующим образом. Если случайные погрешности средств измерений (метода, оператора) представлены средними квадратическими отклонениями 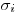 , приведенными в технической документации, среднее квадратическое отклонение результата однократного измерения
, приведенными в технической документации, среднее квадратическое отклонение результата однократного измерения 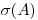 вычисляют по формуле
вычисляют по формуле
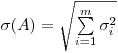 (7.64),
(7.64), где 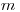 — число составляющих.
— число составляющих.
Доверительную границу случайной погрешности результата измерения 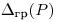 вычисляют по формуле
вычисляют по формуле
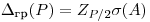 (7.65),
(7.65), где 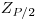 — точка нормирования функции Лапласа, отвечающая вероятности
— точка нормирования функции Лапласа, отвечающая вероятности 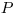 . При доверительной вероятности
. При доверительной вероятности 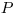 = 0,95
= 0,95 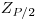 = 2, при
= 2, при 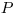 = 0,99
= 0,99 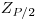 = 2,6.
= 2,6.
Если случайные погрешности средств измерений (метода, оператора) представлены доверительными границами 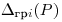 соответствующими одной и той же вероятности, доверительную границу случайной погрешности результата однократного измерения вычисляют по формуле
соответствующими одной и той же вероятности, доверительную границу случайной погрешности результата однократного измерения вычисляют по формуле
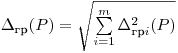 (7.66).
(7.66). Если случайные погрешности средств измерений (метода, оператора) представлены доверительными границами, соответствующими разным вероятностям, сначала определяют среднее квадратическое отклонение результата измерения по формуле
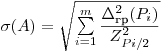 (7.67),
(7.67), а потом вычисляют доверительные границы случайной погрешности результата измерения по формуле
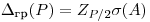 (7.68),
(7.68), Оценивание погрешности результата измерения осуществляют следующим образом:
1. Если погрешости метода и оператора пренебрежимо малы по сравнению с погрешностью используемых средств измерений (не превышают 15%), за погрешность результата измерения принимают погрешность используемых средств измерений.
2. Если 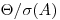 < 0,8, неисключенными систематическими погрешностями пренебрегают и принимают в качестве погрешности результата измерения доверительные границы случайных погрешностей.
< 0,8, неисключенными систематическими погрешностями пренебрегают и принимают в качестве погрешности результата измерения доверительные границы случайных погрешностей.
3. Если 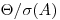 > 8, случайными погрешностями пренебрегают и принимают в качестве погрешности результата измерения границы неисключевлых систематических погрешностей.
> 8, случайными погрешностями пренебрегают и принимают в качестве погрешности результата измерения границы неисключевлых систематических погрешностей.
4. Если 8 ≥ 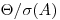 ≥ 8, доверительную границу погрешности результата измерений вычисляют по формуле
≥ 8, доверительную границу погрешности результата измерений вычисляют по формуле
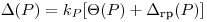 (7.69),
(7.69), где 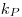 — коэффициент, выбираемый в зависимости от отношения
— коэффициент, выбираемый в зависимости от отношения 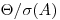 и доверительной вероятности:
и доверительной вероятности:
| 0,8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0,78 | 0,74 | 0,71 | 0,73 | 0,76 | 0,78 | 0,79 | 0,80 | 0,81 |
| 0,84 | 0,82 | 0,80 | 0,81 | 0,82 | 0,83 | 0,83 | 0,84 | 0,85 |
При симметричной доверительной погрешности результат однократного измерения представляется в форме 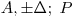 или
или 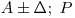 .
.
Числовые значения результата измерения должны оканчиваться цифрами того же разряда, что и значение погрешности.