7.7. Критерии оценивания результатов наблюдений, содержащих грубые погрешности
Критерий Райта
В соответствии с этим критерием результат наблюдения содержит грубую погрешность и должен быть исключен, если его случайное отклонение от среднего арифметического значения превышает величину 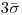 . Причем первоначальной статистической обработке подлежит весь ряд, включая «подозреваемый» результат. Например, если
. Причем первоначальной статистической обработке подлежит весь ряд, включая «подозреваемый» результат. Например, если 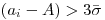 , то
, то 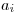 содержит грубую погрешность. Данный критерий можно применять, когда оценка среднего квадратического отклонения
содержит грубую погрешность. Данный критерий можно применять, когда оценка среднего квадратического отклонения 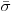 определяется на основании достаточно большого числа результатов наблюдений (
определяется на основании достаточно большого числа результатов наблюдений (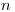 > 20).
> 20).
Критерий Романовского
В соответствии с этим критерием результат наблюдения содержит грубую погрешность и должен быть исключен, если его случайное отклонение от среднего арифметического значения превышает некоторое значение 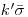 , где
, где 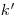 — безразмерный коэффициент, выбираемый в зависимости от числа наблюдений и уровня значимости
— безразмерный коэффициент, выбираемый в зависимости от числа наблюдений и уровня значимости 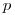 . При этом первоначальной статистической обработке подвергаются только те результаты, которые не вызывают сомнений. Таким образом, если
. При этом первоначальной статистической обработке подвергаются только те результаты, которые не вызывают сомнений. Таким образом, если 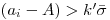 ,
, 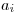 содержит грубую погрешность. Данный критерий рекомендуется применять, когда оценка среднего квадратического отклонения определяется на основании небольшого числа результатов наблюдений (
содержит грубую погрешность. Данный критерий рекомендуется применять, когда оценка среднего квадратического отклонения определяется на основании небольшого числа результатов наблюдений (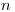 < 20).
< 20).
Число результатов наблюдения | Уровень значимости | |||
|---|---|---|---|---|
0,05 | 0,02 | 0,01 | 0,005 | |
2 | 15,56 | 38,97 | 77,96 | 779,70 |
3 | 4,97 | 8,04 | 11,46 | 36,50 |
4 | 3,56 | 5,08 | 6,53 | 14,46 |
5 | 3,04 | 4,10 | 5,04 | 9,43 |
6 | 2,73 | 3,64 | 4,36 | 7,41 |
7 | 2,62 | 3,36 | 3,96 | 6,37 |
8 | 2,51 | 3,18 | 3,71 | 5,73 |
9 | 2,43 | 3,05 | 3,54 | 5,31 |
10 | 2,37 | 2,96 | 3,41 | 5,01 |
11 | 2,33 | 2,89 | 3,31 | 4,79 |
12 | 2,29 | 2,83 | 3,23 | 4,62 |
13 | 2,26 | 2,78 | 2,17 | 4,48 |
14 | 2,24 | 2,74 | 3,12 | 4,37 |
15 | 2,22 | 2,71 | 3,08 | 4,28 |
16 | 2,20 | 2,68 | 3,04 | 4,20 |
17 | 2,18 | 2,66 | 3,01 | 4,13 |
18 | 2,17 | 2,64 | 3,00 | 4,07 |
19 | 2,16 | 2,62 | 2,95 | 4,02 |
20 | 2,145 | 2,60 | 2,93 | 3,98 |
Критерий Граббса
В соответствии с этим критерием результат наблюдения содержит грубую погрешность и должен быть исключен, если частное 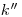 от деления его случайного отклонения от среднего арифметического значения на оценку среднего квадратического отклонения результатов наблюдений
от деления его случайного отклонения от среднего арифметического значения на оценку среднего квадратического отклонения результатов наблюдений 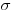 превышает некоторое число
превышает некоторое число 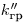 , выбираемое в зависимости от уровня значимости
, выбираемое в зависимости от уровня значимости 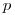 и числа результатов наблюдений
и числа результатов наблюдений 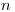 . Если
. Если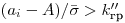 ,
, 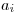 содержит грубую погрешность. Данный критерий основан на предположении о нормальном распределении результатов наблюдений.
содержит грубую погрешность. Данный критерий основан на предположении о нормальном распределении результатов наблюдений.
Число результатов наблюдения | Уровень значимости | |||
|---|---|---|---|---|
0,05 | 0,01 | 0,05 | 0,10 | |
3 | 1,414 | 1,414 | 1,414 | 1,412 |
4 | 1,730 | 1,728 | 1,710 | 1,689 |
5 | 1,982 | 1,972 | 1,917 | 1,869 |
6 | 2,183 | 2,161 | 2,067 | 1,996 |
7 | 2,344 | 2,310 | 2,182 | 2,093 |
8 | 2,476 | 2,431 | 2,273 | 2,172 |
9 | 2,586 | 2,532 | 2,349 | 2,238 |
10 | 2,680 | 2,616 | 2,414 | 2,294 |
11 | 2,760 | 2,689 | 2,470 | 2,343 |
12 | 2,830 | 2,753 | 2,519 | 2,387 |
13 | 2,892 | 2,809 | 2,563 | 2,426 |
14 | 2,947 | 2,859 | 2,602 | 2,461 |
15 | 2,997 | 2,905 | 2,638 | 2,494 |
16 | 3,042 | 2,946 | 2,670 | 2,523 |
17 | 3,083 | 2,983 | 2,701 | 2,551 |
18 | 3,120 | 3,017 | 2,728 | 2,577 |
19 | 3,155 | 3,049 | 2,754 | 2,601 |
20 | 3,187 | 3,079 | 2,779 | 2,623 |
21 | 3,217 | 3,106 | 2,801 | 2,644 |
22 | 3,245 | 3,132 | 2,823 | 2,664 |
23 | 3,271 | 3,156 | 2,843 | 2,683 |
24 | 3,295 | 3,179 | 2,862 | 2,701 |
25 | 3,318 | 3,200 | 2,880 | 2,718 |
Следует обратить внимание, что критерии Граббса и Романовского находятся в некотором противоречии друг с другом.