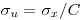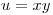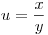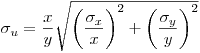7.4.4. Оценка точности результатов косвенных измерений. Закон накопленияпогрешностей
До сих пор речь шла о результатах непосредственных, или прямых, измерений, т.е. таких измерений, при которых непосредственно определяется интересующая нас величина. В экспериментальной работе редко удается ограничиться выполнением прямых измерений, чаще проводятся косвенные измерения, при которых подлежащая определению величина представляет собой некоторую функцию от непосредственно измеряемых величин, отягощенных случайными погрешностями. При измерении скорости счета образца непосредственно определяют суммарную скорость счета препарата с фоном и скорость счета фона. При экспериментальном определении коэффициента регистрации 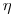 находят отношение скоростей счета образцов, измеренных на данной установке, к их абсолютной активности, определяемой с помощью 4π-счетчика. В подобных случаях возникает задача оценки погрешностей косвенных измерений. Среднее арифметическое и погрешность результата косвенных измерений можно вычислять двояко. Во-первых, можно воспользоваться методами, применяемыми для оценки погрешностей непосредственных измерений. Предположим, что нас интересует некоторая величина
находят отношение скоростей счета образцов, измеренных на данной установке, к их абсолютной активности, определяемой с помощью 4π-счетчика. В подобных случаях возникает задача оценки погрешностей косвенных измерений. Среднее арифметическое и погрешность результата косвенных измерений можно вычислять двояко. Во-первых, можно воспользоваться методами, применяемыми для оценки погрешностей непосредственных измерений. Предположим, что нас интересует некоторая величина 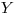 , связанная функциональной зависимостью с величинами
, связанная функциональной зависимостью с величинами 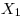 и
и 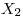 , которые определяются в результате прямых измерений:
, которые определяются в результате прямых измерений: 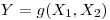 . Пусть процедура измерений организована так, что каждому измерению величины
. Пусть процедура измерений организована так, что каждому измерению величины 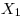 соответствует измерение величины
соответствует измерение величины 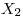 (например, при определении регистрируемой активности препарата чередуют измерения препарата с фоном и фона по схеме: препарат — фон, препарат— фон и т. д.). Тогда по данным каждой пары измерений —
(например, при определении регистрируемой активности препарата чередуют измерения препарата с фоном и фона по схеме: препарат — фон, препарат— фон и т. д.). Тогда по данным каждой пары измерений — 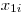 и
и 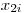 можно рассчитать величину
можно рассчитать величину 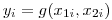 и обычными методами найти среднее арифметическое и погрешность результата косвенных измерений, а также рассчитать доверительные интервалы. Нередко требуется оценить среднее значение и погрешность функции случайных величин, зная лишь средние значения и погрешности независимых переменных. Тогда необходим другой путь расчета среднего арифметического и погрешности результата косвенных измерений, основанный на использовании закона накопления погрешностей. В соответствии с этим законом среднее значение и выборочную дисперсию величины
и обычными методами найти среднее арифметическое и погрешность результата косвенных измерений, а также рассчитать доверительные интервалы. Нередко требуется оценить среднее значение и погрешность функции случайных величин, зная лишь средние значения и погрешности независимых переменных. Тогда необходим другой путь расчета среднего арифметического и погрешности результата косвенных измерений, основанный на использовании закона накопления погрешностей. В соответствии с этим законом среднее значение и выборочную дисперсию величины 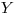 , которая представляет собой функцию
, которая представляет собой функцию 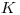 независимых случайных величин
независимых случайных величин 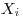
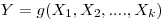 (7.39),
(7.39), можно аппроксимировать выражениями:
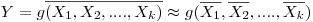 (7.40);
(7.40); 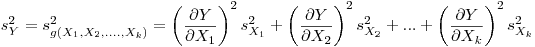 .
.
В последнем выражении 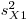 ,
, 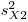 ,....
,.... 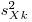 — выборочные дисперсии случайных величин
— выборочные дисперсии случайных величин 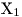 ,
, 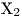 ,...,
,..., 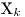 . Заметим, что соотношение (7.40) сохраняет силу и в тех случаях, когда вместо выборочных дисперсий в него подставляют генеральные дисперсии
. Заметим, что соотношение (7.40) сохраняет силу и в тех случаях, когда вместо выборочных дисперсий в него подставляют генеральные дисперсии 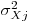 или квадраты погрешностей, вычисленных при выбранном уровне доверительной вероятности
или квадраты погрешностей, вычисленных при выбранном уровне доверительной вероятности 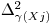 .
.
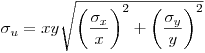
Относительную погрешность результата косвенных измерений можно вычислить по обычной формуле, подобной (6). Бывают случаи, когда легче сразу определить относительную погрешность функции ряда случайных величин. Почленно разделив уравнение на 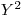 и замечая, что
и замечая, что
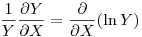 ,
,
получим выражение для относительного выборочного квадратического отклонения результата косвенных измерений:
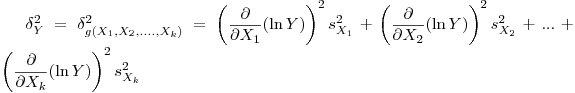 (7.41).
(7.41). В это соотношение вместо выборочных дисперсий можно подставить генеральные дисперсии 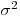 (тогда получится выражение для относительного генерального квадратического отклонения
(тогда получится выражение для относительного генерального квадратического отклонения 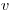 ) или квадраты доверительных погрешностей
) или квадраты доверительных погрешностей 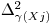 (тогда получится выражение для относительной погрешности значения
(тогда получится выражение для относительной погрешности значения 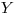 , соответствующей выбранному уровню доверительной вероятности,
, соответствующей выбранному уровню доверительной вероятности, 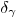 ). Если относительная погрешность вычислена по формуле (7.41), то не имеет смысла прибегать к прямому расчету абсолютной погрешности по формуле (7.40) — ее удобнее определять из очевидного соотношения
). Если относительная погрешность вычислена по формуле (7.41), то не имеет смысла прибегать к прямому расчету абсолютной погрешности по формуле (7.40) — ее удобнее определять из очевидного соотношения
 (7.42).
(7.42). Нетрудно убедиться, что для функций вида
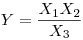 (7.43),
(7.43), относительное выборочное квадратическое отклонение равно
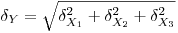 (7.44).
(7.44).
Напомним основные уравнения математической статистики:
| |
| |
| |
| |
| |
| |
| |
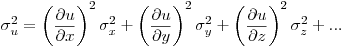

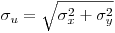
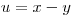
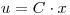 ,
, 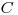 = const
= const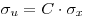
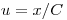 ,
,