7.4.2. Проверка гипотезы о пуассоновском характере распределения результатовизмерения радиоактивности

Доверительный интервал можно рассматривать как интервал значений исследуемого параметра, совместимых с опытными данными и не противоречащих им. Иными словами, событие с вероятностью 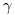(заключающееся, например, в том, что значение генерального параметра находится внутри доверительного интервала) считают практически достоверным, а событие с вероятностью 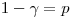– практически невозможным. Эти положения лежат в основе проверки статистических гипотез. Правила, устанавливающие условия, при которых проверяемую гипотезу следует отвергнуть либо отвергать не следует, называют статистическим критерием. Статистические критерии базируются на определенных функциях от выборочных параметров, для которых известны точные законы распределения. Процедура статистической проверки гипотез предусматривает выбор соответствующей функции и построение доверительного интервала для значений этой функции в предположении, что верна проверяемая гипотеза. Границы доверительного интервала являются критическими точками для принятого уровня значимости: если найденное из опыта значение функции 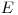от элементов выборки окажется больше критического значения 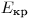, то проверяемую гипотезу отвергают. Обычно ориентируются на 5%-ный уровень значимости ( 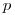= 0,05). Для проверки гипотезы о том, что результаты измерения активности подчиняются распределению Пуассона, используется так называемое χ²-распределение. Это распределение имеет случайная величина

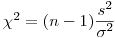(7.36),

которую можно получить на основании выборки из 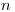элементов, взятых из нормальной совокупности. Как и распределение Стыодента, распределение величины (7.36) зависит только от числа степеней свободы 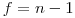. Вероятность того, что случайная величина (7.36) превысит некоторое предельное значение 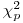, определяется установленным уровнем значимости

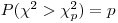(7.37).

Чтобы оценить степень близости наблюдаемого распределения результатов измерения активности к распределению Пуассона, подсчитывают величину 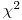подставляя в (7.36) выборочную дисперсию 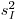, 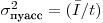и :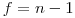

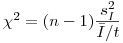(7.38).

Если найденное таким образом экспериментальное значение 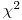(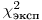) превышает критическое значение для 5%-ного уровня значимости при числе степеней свободы ,

,

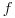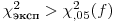то расхождение между эмпирическим и теоретическим (пуассоновским) распределением признают существенным. Отклонение распределения числа регистрируемых импульсов от закона Пуассона свидетельствует о наличии случайных погрешностей, не связанных со статистическим характером распада. В этом случае оценку генерального среднего скорости счета необходимо проводить с помощью t-распределения на основании выборочного среднего квадратического отклонения 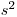, т. е. строить доверительный интервал вида (7.32).

Если 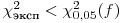, то считают, что нет оснований отвергнуть предположение о том, что число импульсов, регистрируемых детектором за время отдельного измерения, распределено в соответствии с законом Пуассона. Стало быть, рассеяние результатов обусловлено только статистическим характером радиоактивного распада, а другие случайные погрешности, которые в зависимости от постановки эксперимента могут быть связаны с аппаратурными факторами, процедурой измерений, методикой приготовления препаратов и т.п., отсутствуют. В этом случае для оценки генерального среднего следует использовать нормальное распределение и строить доверительный интервал вида (7.29), подставляя в указанную формулу значения 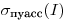из (7.19).