7.4.1. Основные понятия теории интервального оценивания. Оценка генеральногосреднего на основании выборочных данных

Доверительным интервалом неизвестного параметра 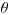называют такой числовой интервал 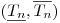, внутри которого с заранее установленной вероятностью 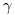может находиться значение 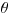, так что

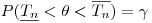(7.23).

Нижнюю 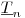и верхнюю 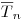границы доверительного интервала называют доверительными границами. Доверительные границы определяются как функции от результатов 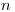измерений, составляющих выборочную совокупность, и, вследствие случайного характера выборки, сами — случайные величины. Поэтому при многократном повторении серии измерений и положение, и ширина доверительных интервалов будут изменяться, однако в 100% случаев доверительные интервалы будут накрывать истинное значение оцениваемого параметра. Вероятность 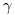того, что интервал 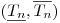содержит в себе истинное значение параметра, называется доверительной вероятностью, а величина

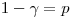(7.24)

– уровнем значимости. Уровень значимости показывает, насколько часто при повторении выборки наше суждение (например, что значение генерального параметра лежит в пределах доверительного интервала) будет оказываться ошибочным. Доверительные интервалы строят обычно для 95%-ной доверительной вероятности (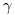 = 0,95; 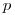= 0,05) или для 99%-ной доверительной вероятности ( 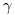= 0,99; 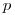= 0,01). При оценивании генеральных параметров берутся симметрично построенные доверительные интервалы, для которых выполняются соотношения

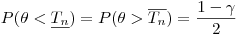(7.25).

Таким образом, задача построения доверительного интервала (7.23) сводится к нахождению нижней и верхней доверительных границ, удовлетворяющих требованию (7.25).

Итак, чем больше значение 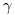, тем выше надежность оценки, но тем больше и ширина доверительного интервала, характеризующая погрешность оценивания. Таким образом, для того чтобы охарактеризовать случайную погрешность измерений, необходимо указать ширину доверительного интервала и доверительную вероятность. Указание одного только доверительного интервала лишено смысла, поскольку его размер зависит от принятого уровня доверительной вероятности. Строя доверительный интервал для 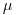на основании отдельного измерения, иногда исходят из того, что результат этого измерения взят из генеральной совокупности с нормальным законом распределения. Вообще, чтобы найти доверительный интервал для генерального параметра на основании какой-либо выборочной характеристики, нужно знать закон распределения этой характеристики. Рассмотрим методы нахождения доверительных интервалов для генерального среднего на основании выборочного среднего. Чтобы построить доверительный интервал для 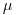исходя из 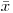, необходимо знать закон распределения средних арифметических. В зависимости от того, располагает ли исследователь знанием генеральной дисперсии 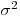, или ему известна лишь ее выборочная оценка 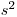, распределение величин 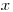подчиняется различным законам. Эти законы изучены для выборок из нормальных совокупностей, с которыми чаще всего приходится иметь дело на практике. 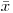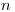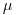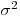Средние арифметические для выборок, которые содержат элементов, взятых из нормальной совокупности с параметрами и , также подчиняются нормальному распределению с тем же самым значением генерального среднего 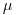и генеральной дисперсией 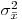, равной

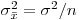(7.26).

Введем вместо случайной величины 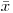нормированную случайную величину

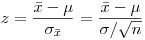(7.27).

Величина 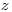распределена по нормальному закону с параметрам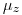и = 0 и 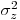= 1. Пользуясь таблицами нормального распределения можно найти два таких числа 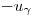и 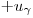, для которых выполняется условие

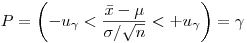(7.28).

Решая неравенство (28) относительно 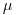, находим

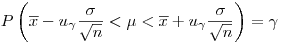(7.29).

Соотношением (7.29), можно пользоваться для интервального оценивания генерального среднего в тех случаях, когда известно значение генеральной дисперсии 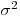. Если значение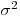не известно, то распределение среднего арифметического отличается от нормального, особенно сильно в тех случаях, когда число измерений 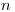мало. Это обусловлено появлением дополнительного источника неопределенности, связанного с тем, что вместо величины 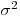приходится пользоваться ее выборочной оценкой 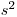, вычисляемой по формулам (7.4) или (7.5), и вместо 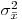– выборочной дисперсией среднего арифметического 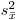, которая, по аналогии с (7.26), определяется выражением

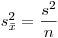(7.30).

В этом случае при построении доверительных интервалов исходят из так называемого распределения Стьюдента, или t-распределения. Это распределение имеет случайная величина

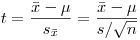(7.31).

Распределение Стьюдента зависит только от числа степеней свободы 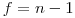, связанного с выборочной дисперсией 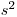. Кривые распределения Стьюдента напоминают по форме кривые нормального распределения, но для малых значений 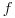они значительно медленнее сближаются с осью абсцисс 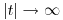при . При 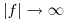t-распределение совпадает с нормальным. Вероятность того, что при доверительной вероятности 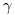случайная величина попадет в симметричный интервал с доверительными границами 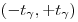, определяется выражением

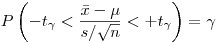(7.32).

Решая неравенства (32) относительно 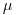, получим

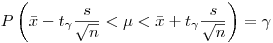(7.33).

Этим соотношением следует пользоваться для интервального оценивания генерального среднего в тех случаях, когда неизвестно значение генеральной дисперсии 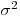. Величины

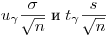(7.34)

называют доверительными погрешностями, или погрешностями среднего арифметического при доверительной вероятности 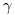и обозначают символом 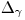. Таким образом, результат измерений следует записывать в виде

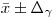(7.35),

указывая при этом принятый уровень доверительной вероятности 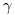. Относительные погрешности среднего арифметического при доверительной вероятности 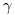будем обозначать символом .

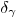Критерий Стьюдента может быть использован для сопоставления выборочного среднего двух серий измерений. Для этого необходимо рассчитать средние скорости счета препарата в каждой серии и выборочные дисперсии отдельного измерения для каждой серии препаратов. Далее по формуле

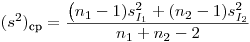(7.35а)

необходимо рассчитать среднее взвешенное дисперсий двух измерений. Число степеней свободы здесь .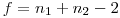

Затем рассчитывают величину

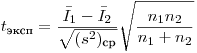(7.35б).

Если найденное значение 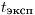по абсолютной величине превышает табличное для 1% уровня значимости, то гипотеза о равенстве генеральных средних отбрасывается. Это означает, что разность между средними значениями скорости счета настолько велика, что не может быть объяснена случайными колебаниями этих величин. Гипотеза ставится под сомнение, если найденное превышает табличное значение для 5% уровня значимости.