7.3. Статистический характер радиоактивного распада и распределениеПуассона

В зависимости от организации эксперимента и процедуры измерений появление случайных погрешностей можно связать с теми или иными конкретными причинами. Так, например, если производят несколько измерений одного и того же препарата, не изменяя его положения, то источником случайных погрешностей могут быть колебания стабилизированного напряжения и (или) величины фона. Если при измерениях поворачивают препарат на некоторый случайный угол, используя цилиндрический счетчик или торцовый счетчик со щелевой диафрагмой, то кроме названных причин на возникновение случайных погрешностей может влиять неравномерность распределения радиоактивного вещества по поверхности препарата и (или) недостаточно четкая фиксация препарата в кассете для измеряемых образцов. Если измеряют серию препаратов, приготовленных из одинаковых объемов радиоактивного раствора, то помимо колебаний стабилизированного напряжения и фона, неоднородности препаратов и смещения их относительно счетчика на рассеяние результатов, возможно, будут оказывать влияние и факторы, связанные с методикой приготовления препаратов (точность определения объемов, неполнота осаждения и т. п.).

Этот перечень можно продолжить и дальше — случайные погрешности возникают на любой стадии проведения эксперимента. Но каковы бы ни были случайные погрешности, искажающие результат отдельного измерения, в каждый результат вносится погрешность, обусловленная статистическим характером радиоактивного распада. Радиоактивные превращения — это процесс, которому присущ вероятностный характер. Законы радиоактивного распада и накопления — статистические законы, проявляющиеся лишь для достаточно большого числа радиоактивных ядер. Основные предположения, на основании которых можно найти закономерности, характеризующие вероятностную природу радиоактивного распада, заключаются в следующем.

1. Вероятность 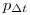распада отдельного ядра за время 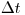не зависит от условий, в которых ядро находилось ранее или находится в данное время, а зависит только от размера интервала 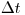и для достаточно малых отрезков времени пропорциональна 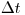: 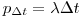(здесь 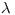— коэффициент пропорциональности).
2. Вероятность 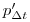того, что одно из 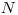ядер распадется в течение бесконечно малого интервала времени 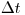, пропорциональна 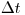и наличному количеству ядер: 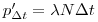, или, принимая во внимание, что ожидаемое среднее число распадов в единицу времени , .
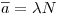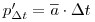3. Вероятность того, что за промежуток времени 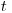, малый по сравнению с периодом полураспада, распадется 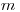ядер, не зависит от того, какое количество ядер распалось в предшествующие промежутки времени равного размера.

Первое условие приводит к основному закону радиоактивного распада. Действительно, если вероятность распада отдельного ядра за время 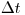определяется условием 1, то вероятность противоположного события (того, что ядро не распадется за это время) равна

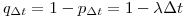(7.8).

Но если ядро не распалось в течение времени 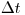, то вероятность того, что оно не распадется в течение второго такого же интервала времени, снова равна 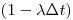. Вероятность же того, что ядро не распадется ни в первый, ни во второй интервалы времени, равна произведению этих вероятностей; рассуждая и далее подобным образом, получим

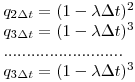(7.9)

Интервал 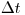можно представить как 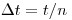(промежуток времени 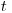делится на 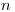не перекрывающихся интервалов размером 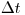). Переходя к пределу при 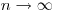, найдем вероятность того, что отдельное ядро не претерпит распада в течение времени :

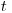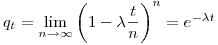(7.10).

Из определения вероятности следует, что при многократном повторении испытаний отношение числа ядер 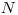, не распавшихся за время 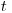, к числу ядер в начальный момент времени 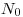должно колебаться около величины 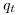так что можно записать

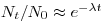(7.11).

Мы пришли к интегральной форме закона радиоактивного распада

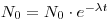(7.12),

но теперь ясно видно, что в силу статистического характера этого закона он должен выполняться лишь приближенно. Экспоненциальный характер закона распада проявляется в результате усреднения случайных отклонений числа распадающихся ядер от теоретически ожидаемого. Это можно проиллюстрировать рис. 1, на котором в полулогарифмическом масштабе нанесены результаты измерения скорости счета при определении периода полураспада ⁵⁶Мn (продолжительность каждого измерения 1 мин, интервал между измерениями 2 мин). Исходя из условий 2и 3, можно вывести закон, определяющий вероятности 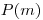того, что в течение промежутка времени 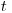произойдет 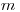актов распада, если среднее число актов распада за время 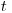равно :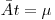

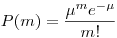(7.13).

Рис. 7.1. Статистический характер закона радиоактивного распада

Такое распределение вероятностей называется распределением Пуассона. В выражение (13) входит только один параметр (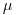), от которого зависит вид кривой пуассоновского распределения. Как уже было сказано, 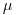— это среднее значение случайной величины (в данном случае величины, распределенной по закону Пуассона); замечательно, что дисперсия распределения Пуассона также равна :

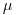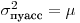(7.14).

На рис. 7.1 показаны кривые распределения Пуассона для 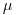равным 1, 5 и 10. Заметим, что в отличие от нормального распределения распределение Пуассона дискретно: величины 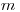могут принимать лишь положительные целочисленные значения. Поэтому было бы правильнее изображать вероятности появления каждого значения 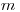вертикальными отрезками. Однако для наглядности на рис. 7.2 через точки, соответствующие вероятностям 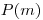, проведены плавные кривые.) Из рисунка видно, что при малых значениях 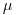распределение Пуассона асимметрично (максимум смещен влево), но по мере роста 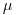кривые становятся все более симметричными, приближаясь к виду кривой нормального распределения. Практически уже при 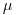= 10 распределение Пуассона достаточно хорошо аппроксимируется нормальным распределением, оба параметра которого равны .

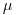Рис. 7.2. Вид распределения Пуассона для различных значений m

Если рассеяние результатов вызвано лишь статистическим характером распада, то распределение числа импульсов 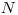, регистрируемых детектором за время 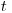, также подчиняется закону Пуассона. А именно, вероятность 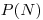того, что за выбранный промежуток времени будет зарегистрировано 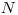имп. если среднее число регистрируемых импульсов составляет 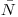, определяется выражением

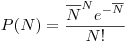(7.15).

По аналогии с (14) дисперсия пуассоновского распределения числа регистрируемых прибором импульсов равна

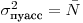(7.16).

Соответствующее среднее квадратическое отклонение называют иногда абсолютной квадратической флуктуацией, чтобы подчеркнуть его природу. Если в единичном опыте зарегистрировано достаточно большое число импульсов 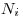, то для определения среднего квадратического отклонения вместо 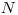можно использовать 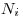. Таким образом

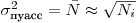(7.17).

Как уже говорилось, величина 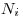в формуле (17) представляет собой число импульсов, зарегистрированных прибором за 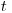мин. В таком случае скорость счета равна

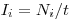(7.18).

Среднее квадратическое отклонение скорости счета, обусловленное статистическим характером распада (абсолютная квадратическая флуктуация), составляет

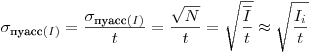(7.19),

а относительная квадратическая флуктуация равна

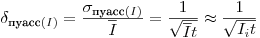(7.20).

Из формулы (7.20) следует, что величина относительных погрешностей, связанных со статистическим характером распада, уменьшается с увеличением регистрируемой скорости счета 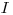и продолжительности отдельного измерения 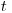. Погрешность, связанная с флуктуациями радиоактивного распада, входит в выборочное среднее квадратическое отклонение 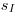, которое можно рассчитать по следующим формулам:

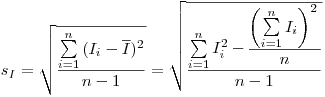(7.21).

Величина 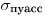определяет минимально возможное среднее квадратическое отклонение при заданных значениях 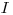и 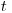. Таким образом, в отсутствие иных источников рассеяния, кроме статистического характера радиоактивного распада,

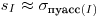(7.22).

Вследствие того, что выборочное среднее квадратическое отклонение 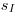— случайная величина, его значение в некоторых опытах может оказаться меньше, чем 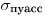. Однако всегда следует иметь в виду, что 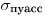характеризует минимально возможное рассеяние значений скорости счета в генеральной совокупности, отвечающей выбранным условиям эксперимента.