7.2. Генеральная и выборочная совокупность. Расчет среднего и дисперсии повыборочным данным

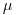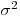Представим себе, что при данных условиях выполнено бесконечно большое число измерений одной и той же величины. Полученную бесконечную гипотетическую совокупность результатов называют генеральной совокупностью. Величины и — параметры генеральной совокупности; их точные значения можно было бы найти, зная лишь все элементы генеральной совокупности. Истинное значение измеряемой величины 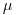, называемое генеральным средним, равно

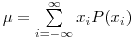(7.1),

где 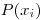— вероятность появления результата 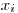. (Отрицательные значения i характеризуют те результаты измерений, которые были получены ранее некоторого условного момента, принятого за начало отсчета.) Параметр 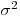представляет собой генеральную дисперсию. Генеральная дисперсия определяется равенством

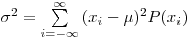(7.2).

Любую совокупность результатов измерений, выполненных при данных условиях опыта, принято рассматривать как случайную выборку из генеральной совокупности, т.е. как выборочную совокупность. (В экспериментаторской практике опыты, результаты которых составляют выборочную совокупность, называют обычно параллельными.) Выборочная совокупность характеризуется значениями выборочных параметров, которые являются функциями величин, составляющих выборочную совокупность. Чтобы четко разграничивать генеральные и выборочные параметры, для обозначения генеральных параметров используют греческие буквы, а выборочных — латинские. Выборочное среднее определяют как среднее арифметическое 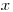из 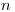результатов измерений:

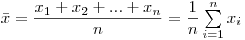(7.3).

Выборочную дисперсию обозначают через 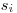и вычисляют по формуле

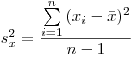(7.4)

или по эквивалентной ей формуле

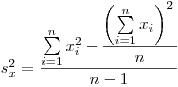(7.5).

Знаменатель в выражениях (7.4) и (7.5) характеризует число степеней свободы для выборочной дисперсии. Число степеней свободы 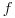равно числу независимых измерений минус число дополнительных связей, налагаемых на экспериментальный материал в процессе его обработки. Так, на 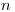независимых результатов измерений при расчете среднего арифметического накладывается одна связь вида (3), поэтому число степеней свободы при определении выборочной дисперсии .

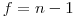Нередко для характеристики разброса (рассеяния) данных указывают относительную погрешность, которая определяется как отношение соответствующей абсолютной погрешности к среднему значению измеряемой величины.

Относительное выборочное квадратическое отклонение равно

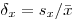(7.6).

При обработке результатов эксперимента необходимо всегда помнить о различии между генеральными и выборочными параметрами. Генеральные параметры являются постоянными, характеризующими закон распределения случайных величин (результатов измерений, отягощенных случайными погрешностями), в то время как выборочные параметры сами суть случайные величины. Поэтому имеют место лишь приближенные равенства:

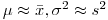(7.7),

которые выполняются тем точнее, чем больше число проведенных измерений. Величины 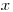и 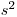представляют собой точечные оценки генеральных параметров, однако приближенные равенства (7.7) не дают представления о точности, с которой установлены значения 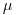и 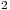. Поэтому при обработке экспериментальных данных используются методы интервального оценивания, позволяющие рассчитывать границы интервала, внутри которого с заданной вероятностью может находиться значение генерального параметра. Ширина такого интервала (или половина его ширины) определяет точность результата измерений, а вероятность того, что оцениваемый параметр будет лежать в пределах этого интервала, характеризует надежность оценки. Методы интервального оценивания будут рассмотрены ниже.