3.4.2. Замедление и диффузия нейтронов
Ослабление быстрых нейтронов (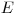 ≥ 1 МэВ) слоем вещества толщиной
≥ 1 МэВ) слоем вещества толщиной 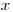 может быть приближенно описано экспоненциальным законом
может быть приближенно описано экспоненциальным законом
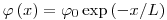 (3.89),
(3.89), где длина релаксации 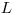 зависит от энергии падающих нейтронов с плотностью потока
зависит от энергии падающих нейтронов с плотностью потока 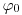 , от геометрии и состава материала защиты и от диапазона энергий за защитой. Таблица 3.5 содержит несколько примеров длин релаксации нейтронов деления в различных материалах.
, от геометрии и состава материала защиты и от диапазона энергий за защитой. Таблица 3.5 содержит несколько примеров длин релаксации нейтронов деления в различных материалах.
Таблица 3.5
Длина релаксации 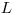 нейтронов деления, проходящих через плоский слой защиты толщиной
нейтронов деления, проходящих через плоский слой защиты толщиной 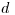 (за слоем нейтроны с энергиями >
(за слоем нейтроны с энергиями >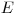 )
)
Преобладающими эффектами взаимодействия для быстрых нейтронов являются упругое и неупругое рассеяние. Взаимодействие нейтронов деления с веществом аппроксимируется экспоненциальным законом ослабления для мощности дозы 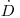 (или дозы
(или дозы 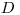 ):
):
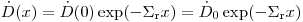 (3.90),
(3.90), где 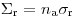 представляет эффективное макроскопическое сечение выведения. Микроскопическое сечение выведения может быть приблизительно выражено через сечения упругого и неупругого рассеяния:
представляет эффективное макроскопическое сечение выведения. Микроскопическое сечение выведения может быть приблизительно выражено через сечения упругого и неупругого рассеяния:
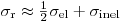 (3.91).
(3.91). В таблице 3.6 приведены сечения выведения для различных материалов. Теория выведения часто используется в качестве первого приближения для расчета защиты от нейтронов.
Таблица 3.6
Сечение выведения 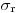 для нейтронов деления
для нейтронов деления
На пути прохождения через рассеивающую среду нейтроны испытывают множество столкновений, поэтому их энергия значительно уменьшается. Этот процесс называется замедлением нейтронов. Основной задачей теории замедления является определение распределения плотности потока нейтронов по энергии и направлению 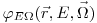 в рассевающей среде для заданного распределения источников
в рассевающей среде для заданного распределения источников 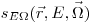 . Сперва определяется плотность замедления
. Сперва определяется плотность замедления 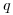 . Она определяет число нейтронов на единицу объема и единицу времени, замедленных с энергий
. Она определяет число нейтронов на единицу объема и единицу времени, замедленных с энергий 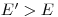 до
до 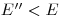 . Из общего уравнения переноса можно получить дифференциальное уравнение для плотности замедления; оно называется возрастным уравнением (см. [16]). Используя его можно определить, например, число нейтронов на единицу объема и единицу времени, замедленных с энергии источника
. Из общего уравнения переноса можно получить дифференциальное уравнение для плотности замедления; оно называется возрастным уравнением (см. [16]). Используя его можно определить, например, число нейтронов на единицу объема и единицу времени, замедленных с энергии источника  до заданной энергии
до заданной энергии 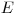 . Более того, можно определить пространственно-энергетическое распределение замедленных нейтронов. В разделе 3.3.1 в качестве решения общего уравнения переноса был получен
. Более того, можно определить пространственно-энергетическое распределение замедленных нейтронов. В разделе 3.3.1 в качестве решения общего уравнения переноса был получен 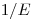 спектр промежуточных нейтронов для частного случая непоглощающей бесконечной водородосодержащей рассеивающей среды. Если условия для среды не полностью выполняются, появляются отклонения от спектра
спектр промежуточных нейтронов для частного случая непоглощающей бесконечной водородосодержащей рассеивающей среды. Если условия для среды не полностью выполняются, появляются отклонения от спектра 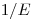 , определяемые параметром
, определяемые параметром 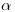 в соответствии с
в соответствии с
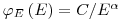 (3.92).
(3.92). Промежуточные нейтроны в конченом счете теряют при замедлении столько энергии, что входят в тепловое равновесие с атомами замедлителя. Спектр этих тепловых нейтронов (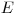 < 0.4 эВ) описывается максвелловским распределением. Если плотность замедления
< 0.4 эВ) описывается максвелловским распределением. Если плотность замедления 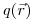 для случая замедления быстрых нейтронов до тепловых энергий в точке
для случая замедления быстрых нейтронов до тепловых энергий в точке 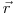 известна, то с помощью элементарной теории диффузии можно вычислить пространственное распределение плотности потока тепловых нейтронов. Уравнение диффузии имеет вид
известна, то с помощью элементарной теории диффузии можно вычислить пространственное распределение плотности потока тепловых нейтронов. Уравнение диффузии имеет вид
 (3.93).
(3.93). Здесь 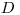 – коэффициент диффузии,
– коэффициент диффузии, 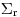 – макроскопическое сечение поглощения. Обе величины представляют собой средние значения по максвелловскому спектру тепловых нейтронов. Для упрощения вводится диффузионная длина
– макроскопическое сечение поглощения. Обе величины представляют собой средние значения по максвелловскому спектру тепловых нейтронов. Для упрощения вводится диффузионная длина
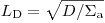 (3.94).
(3.94). Уравнение диффузии (3.93) можно также использовать для вычисления распределения 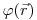 в окрестности источника тепловых нейтронов. В этом случае
в окрестности источника тепловых нейтронов. В этом случае 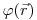 = 0. В зависимости от формы нейтронного источника, для решения уравнения диффузии можно воспользоваться различными подходами. Например, для точечного источника на расстоянии
= 0. В зависимости от формы нейтронного источника, для решения уравнения диффузии можно воспользоваться различными подходами. Например, для точечного источника на расстоянии 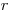
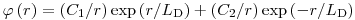 (3.95).
(3.95). Константа  определяется из граничного условия
определяется из граничного условия  при
при 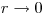 . Плотность потока тепловых нейтронов связана с плотностью тока нейтронов
. Плотность потока тепловых нейтронов связана с плотностью тока нейтронов  соотношением
соотношением
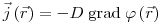 (3.96),
(3.96), тогда для точечного источника
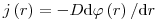 (3.97).
(3.97). Так как связь с мощностью источника 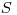 задается как
задается как
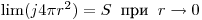 (3.98),
(3.98), то константу 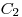 , а с ней и распределение плотности потока
, а с ней и распределение плотности потока 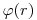 , можно определить подстановкой уравнения (3.95) в уравнения (3.97) и (3.98).
, можно определить подстановкой уравнения (3.95) в уравнения (3.97) и (3.98).
Замедление и диффузия нейтронов связаны с множеством процессов изменения направления движения, поэтому в результате взаимодействия в слое некоторые нейтроны могут покинуть его через плоскость, на которую падают первичные нейтроны. Обратное рассеяние нейтронов и его взаимодействие с полем излучения перед защитой рассматривается в разделе 3.5.1.