3.4.1. Поглощение и рассеяние заряженных частиц

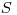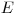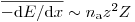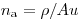Выделение энергии заряженной частицы при прохождении слоя вещества характеризуется средней потерей энергии на элементе пути (величина введена в разделе 3.1.2), также называемой линейной тормозной способностью . Потери энергии вследствие ионизационных эффектов преобладают для частиц с энергиями < 10 МэВ. Так как , где (уравнение (3.10)), то энергия, отнесенная к массе на площадь 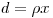, равна

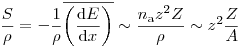(3.79).

Величина, определяемая уравнением (3.79), называется массовой тормозной способностью. Отношение 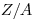мало изменяется в пределах периодической системы, поэтому массовая тормозная способность практически не зависит от вещества, если только атомные номера не различаются слишком сильно. В таблице 3.4 собраны данные по массовым тормозным способностям для электронов в различных веществах в зависимости от энергии.

Таблица 3.4

Массовая тормозная способность 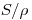(МэВ·см2·г–1) как функция энергии электрона 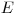(МэВ)

Пробег тяжелых заряженных частиц может быть вычислен из тормозной способности:

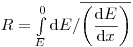(3.80),

что примерно соответствует длине траектории частицы. Для практических целей обычно используют числовые уравнения. Например, для α-частицы с энергией более 2.5 МэВ в воздухе

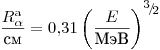(3.81).

Отсюда пробег в веществе с плотностью 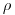и относительной атомной или молекулярной массой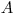

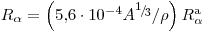(3.82).

Здесь значения 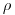и 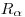подставляются соответственно в г·см–3 и см. Пробег протонов с энергиями выше 0.6 МэВ находится из уравнения

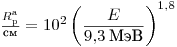(3.83).

Пробег электронов в различных веществах нельзя просто вычислить, так как путь электрона не соответствует прямой линии из-за многократного рассеяния. Поэтому длина траектории гораздо больше пробега. Часто пробег определяют экспериментально и выводят эмпирические зависимости пробега от энергии. Например, для энергий электронов 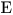> 0.6 МэВ

(3.84).

Если кроме моноэнергетических электронов рассматривать β-частицы от радионуклидного источника с распределением энергии от 0 до 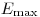, количество 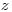зарегистрированных частиц в единицу времени будет уменьшаться приблизительно экспоненциально с ростом толщины слоя, т.е.

(3.85).

Величина называется линейным коэффициентом поглощения. Закон поглощения также может иметь форму

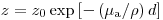(3.86),

где 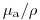– массовый коэффициент поглощения. Толщина половинного поглощения, т.е. толщина слоя, при котором скорость счета уменьшается до 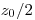, может быть определена из уравнения (3.86) как

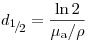(3.87).

Кривая поглощения отклоняется от экспериментальной кривой для 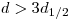(см. рис. 3.13). Наблюдается переход к некоторому фоновому значению, вызванному сопутствующим γ-излучением, как тормозным, так и природным и космическим. Максимальный пробег 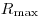β-частиц может быть определен вычитанием этого фона, так как кривая поглощения асимптотически приближается к вертикальной прямой линии в точке 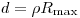. Зависимость максимального пробега от максимальной энергии β-излучения выражается формулой Фламмерсфельда:

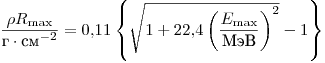(3.88).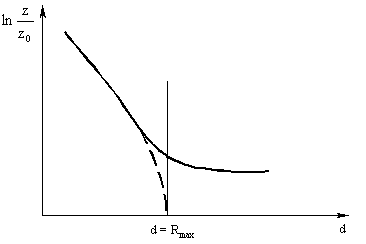

Рис. 3.13. Типичная кривая поглощения для β-излучения

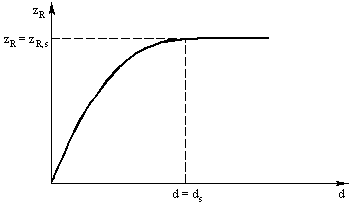
Рис. 3.14. Типичная кривая обратного рассеяния для β-излучения

Полное отклонение β-частиц при рассеянии может быть настолько большим, что частицы в результате нескольких процессов рассеяния могут покинуть вещество через поверхность, на которую они падали. Это называется обратным рассеянием. Обратнорассеянное излучение содержит значительно бóльшую долю низкоэнергетических частиц, чем первичное излучение. Такое изменение к меньшим энергиям более выражено для рассеивающих веществ с малым атомным номером. Скорость счета 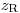обратнорассеянных β-частиц увеличивается с ростом толщины слоя, как показано на рис. 3.14, до некоторого значения насыщения 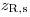. Теоретически насыщение должно наступать при 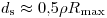, но, как правило, достигается уже при . Толщина насыщения 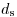увеличивается с ростом энергии β-частиц. В первом приближении скорость счета насыщенного обратнорассеянного излучения увеличивается пропорционально квадратному корню атомного номера; отсюда следует, что для снижения обратнорассеянного β-излучения необходимо использовать материалы с минимально возможным атомным номером.