3.3.3. Численные решения
Для различных задач можно получить аналитические асимптотические решения, сделав значительные упрощения. К этой группе относятся, например, интегральные преобразования, матричные вычисления и разложения на асимптотические последовательности. Более общие задачи требуют применения численных методов.
Одним из примеров является метод последовательных рассеяний, где выполняется разложение по кратности рассеяния. Вклады от нерассеянных, однократно, двукратно и т.д. рассеянных частиц в распределение плотности потока по энергиям и направлениям в точке 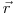 вычисляются отдельно и затем суммируются. Другим методом решения уравнения переноса является точечное приближение. Поле излучения заменяется множеством точечных источников, и плотность потока в точке
вычисляются отдельно и затем суммируются. Другим методом решения уравнения переноса является точечное приближение. Поле излучения заменяется множеством точечных источников, и плотность потока в точке 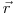 определяется по наложению вкладов от всех источников. Также часто применяется метод дискретных ординат. Здесь весь энергетический диапазон разбивается на энергетические группы, а координатная сетка на локальные и угловые координаты (дискретные ординаты). Интеграл уравнения переноса аппроксимируется групповыми константами для каждой такой ячейки с учетом связей между энергией и углу рассеяния в каждой ячейки решетки. Средняя плотность потока может быть определена для каждой ячейки с соблюдением граничных условий. Метод дискретных ординат обычно приводит к системе из 103 – 104 уравнений, решение которой требует дорогих итерационных методов, а, следовательно, использования производительных компьютеров. Известными программами для решения уравнения переноса с использованием метода дискретных ординат являются ANISN и DOT.
определяется по наложению вкладов от всех источников. Также часто применяется метод дискретных ординат. Здесь весь энергетический диапазон разбивается на энергетические группы, а координатная сетка на локальные и угловые координаты (дискретные ординаты). Интеграл уравнения переноса аппроксимируется групповыми константами для каждой такой ячейки с учетом связей между энергией и углу рассеяния в каждой ячейки решетки. Средняя плотность потока может быть определена для каждой ячейки с соблюдением граничных условий. Метод дискретных ординат обычно приводит к системе из 103 – 104 уравнений, решение которой требует дорогих итерационных методов, а, следовательно, использования производительных компьютеров. Известными программами для решения уравнения переноса с использованием метода дискретных ординат являются ANISN и DOT.
Тогда как эти численные применимы, как правило, только для одномерных или с некоторыми ограничениями для двумерных задач, вследствие больших вычислительных затрат, метод Монте-Карло позволяет решать даже трехмерные задачи. Это метод «теоретического эксперимента», отслеживающий состояние 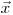 произвольно выбранной частицы на ее пути в среде. Функция
произвольно выбранной частицы на ее пути в среде. Функция 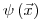 находится как ожидаемое значение функции распределения состояний частицы в заданной точке
находится как ожидаемое значение функции распределения состояний частицы в заданной точке 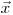 в пространстве состояний, с использованием большого числа вычисленных траекторий частицы, называемых жизненными циклами.
в пространстве состояний, с использованием большого числа вычисленных траекторий частицы, называемых жизненными циклами.
Жизненный цикл характеризуется различными случайными числами 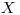 . Плотность
. Плотность 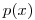 вероятности того, что случайное число примет значение
вероятности того, что случайное число примет значение  , может быть выведена из физических законов переноса излучения, которые были описаны ранее. Должны выполнятся условия
, может быть выведена из физических законов переноса излучения, которые были описаны ранее. Должны выполнятся условия
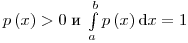 (3.60),
(3.60), где 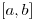 – интервал, в котором находится случайное число
– интервал, в котором находится случайное число 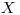 . Плотность вероятности является константой, поэтому случайная величина
. Плотность вероятности является константой, поэтому случайная величина 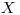 равномерно распределена. Если интервалом является
равномерно распределена. Если интервалом является 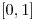 , случайная величина обозначается через
, случайная величина обозначается через 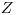 . Таким образом, случайная величина равновероятно принимает любые значения от 0 до 1. Случайные числа в простейших случаях могут определятся с помощью костей или колеса рулетки (с последующей нормировкой на 1). В методе Монте-Карло они генерируются компьютерами по определенным алгоритмам (генераторы случайных чисел).
. Таким образом, случайная величина равновероятно принимает любые значения от 0 до 1. Случайные числа в простейших случаях могут определятся с помощью костей или колеса рулетки (с последующей нормировкой на 1). В методе Монте-Карло они генерируются компьютерами по определенным алгоритмам (генераторы случайных чисел).
Определение случайных величин 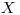 из заданных распределений вероятности
из заданных распределений вероятности 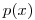 осуществляется с помощью преобразований случайных чисел. Этот процесс называется дискретизацией и выполняется в соответствии с выражением:
осуществляется с помощью преобразований случайных чисел. Этот процесс называется дискретизацией и выполняется в соответствии с выражением:
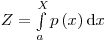 (3.61).
(3.61). В зависимости от случайного значения 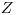 отсюда находится случайная величина. Так как интеграл в уравнении (3.61) на интервале от
отсюда находится случайная величина. Так как интеграл в уравнении (3.61) на интервале от 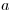 до
до 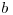 принимает значение 1, то (см. рис. 3.9) для
принимает значение 1, то (см. рис. 3.9) для 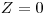 значение
значение 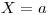 и для
и для 
 .
.
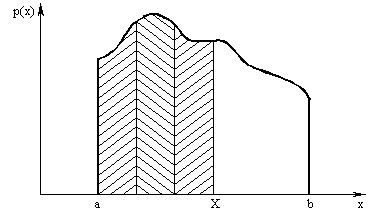
Рис. 3.9. Определение непрерывных случайных величин.
Если интеграл по 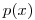 трудно берется или функция
трудно берется или функция 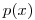 задана графически, то для дискретизации можно воспользоваться методом вон Неймана (см. рис. 3.10). Для этого выбираются два случайных числа
задана графически, то для дискретизации можно воспользоваться методом вон Неймана (см. рис. 3.10). Для этого выбираются два случайных числа 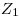 и
и 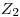 , и строится случайная точка
, и строится случайная точка 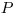 с координатами
с координатами 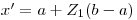 и
и 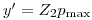 . Если точка
. Если точка 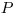 лежит ниже кривой
лежит ниже кривой 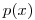 , то необходимой случайной величиной является
, то необходимой случайной величиной является  . В противном случае необходимо повторить построение с новой парой случайных чисел. Случайные числа часто также принимают дискретные значения
. В противном случае необходимо повторить построение с новой парой случайных чисел. Случайные числа часто также принимают дискретные значения 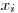 с вероятностями
с вероятностями 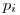 . Тогда, по аналогии с выражением (3.60),
. Тогда, по аналогии с выражением (3.60),
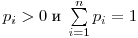 (3.62).
(3.62). Дискретизация осуществляется в соответствии со схемой, показанной на рис. 3.11.
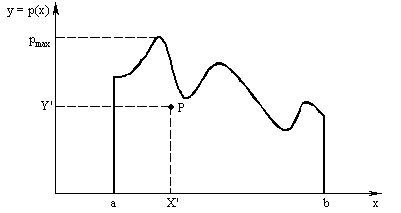
Рис. 3.10. Определение непрерывных случайных величин с помощью метода вон Неймана
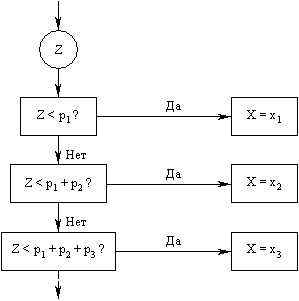
Рис. 3.11. Блок-схема определения дискретных случайных величин
Применение метода Монте-Карло для решения уравнения переноса излучения требует, прежде всего, определения плотностей вероятностей 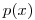 , нормированных на единицу для случайных величин
, нормированных на единицу для случайных величин 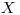 , определяющих жизненный цикл радиационной частицы. Затем определяются случайные значения
, определяющих жизненный цикл радиационной частицы. Затем определяются случайные значения 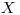 с помощью дискретизации в соответствии с одним из описанных методов.
с помощью дискретизации в соответствии с одним из описанных методов.
Любое моделирование процесса переноса излучения начинается с определения начального состояния, т.е. начального положения, начального направления и начальной энергии, определяемых случайным образом из соответствующих функций распределения. В качестве примера описан процесс дискретизации направления из изотропного распределения по направлениям. С использованием величин, введенных на рис. 3.12, имеем
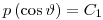 (3.63)
(3.63)и
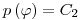 (3.64),
(3.64), где  и
и 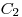 – константы. В результате нормировки плотностей вероятности, т.е.
– константы. В результате нормировки плотностей вероятности, т.е.
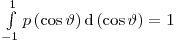 (3.65)
(3.65)и
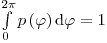 (3.66),
(3.66), получаем 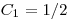 и
и 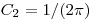 . Поэтому для каждого нового случайного числа
. Поэтому для каждого нового случайного числа 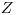 , в соответствии с уравнением (3.61),
, в соответствии с уравнением (3.61),
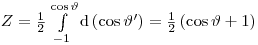 (3.67)
(3.67)и
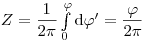 (3.68).
(3.68). Поэтому случайными дискретами, характеризующими направление частицы, являются
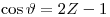 (3.69)
(3.69)и
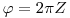 (3.70).
(3.70). 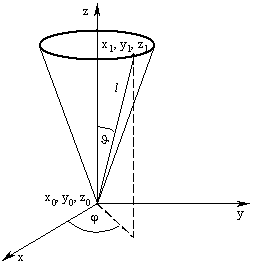
Рис. 3.12. Параметры для вычисления жизненного цикла радиационной частицы
Если все начальные условия определены, следующим шагом моделирования жизненного цикла радиационной частицы является определение точки первого взаимодействия. Она зависит от длины свободного пробега 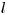 частицы с энергией
частицы с энергией 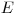 , плотность вероятности для которого давалась в разделе 3.2. Дискретизация осуществляется в соответствии с
, плотность вероятности для которого давалась в разделе 3.2. Дискретизация осуществляется в соответствии с
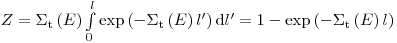 (3.71),
(3.71), тогда
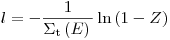 (3.72).
(3.72). Координаты первого взаимодействия:
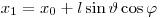 (3.73)
(3.73)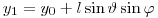 (3.74)
(3.74) (3.75)
(3.75)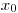 ,
, 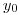 и
и 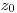 – начальные координаты частицы. Дальнейшая история жизни частицы определяется видом взаимодействия. Этот вид определяется дискретной случайной величиной, вероятность i-го процесса с соответствующим сечением
– начальные координаты частицы. Дальнейшая история жизни частицы определяется видом взаимодействия. Этот вид определяется дискретной случайной величиной, вероятность i-го процесса с соответствующим сечением 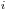 :
:
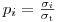 (3.76).
(3.76). Если
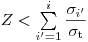 (3.77),
(3.77), где i = 1, 2…n, происходит i-ый процесс взаимодействия. Если это поглощение, то путь частицы завершается, и начинается новый жизненный цикл вычислением начального состояния. Если имеет место процесс рассеяния, то необходимо определить направление и энергию радиационной частицы после рассеяния. Функция плотности для косинуса угла рассеяния находится из дифференциального сечения рассеяния:
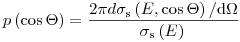 (3.78).
(3.78). После дискретизации 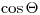 , отсюда можно определить новую энергию, либо с помощью теории сохранения энергии и импульса, либо дискретизацией функции распределения. Затем из угла рассеяния
, отсюда можно определить новую энергию, либо с помощью теории сохранения энергии и импульса, либо дискретизацией функции распределения. Затем из угла рассеяния 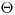 в заданной системе координат вычисляется новое направление движения частицы (координаты
в заданной системе координат вычисляется новое направление движения частицы (координаты 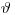 и
и 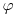 ).
).
Состояние радиационной частицы полностью описывается расположением, энергией и направлением движения. Вычисления по методу Монте-Карло продолжаются определением точки второго взаимодействия. Эти процедуры повторяются до тех пор, пока частица не поглотится или не достигнет такого состояния, дальнейшая обработка которого не нужна, например, после попадания в заданную точку детектора или на граничную поверхность защиты. Энергетическо-угловое распределение плотности потока или производные величины определяются из огромного числа жизненных циклов, вычисляемых с помощью классификации частиц в заданной точке по определенным энергетическим и угловым интервалам.
Точность результатов можно повысить введением взвешенных плотностей вероятности, тогда особенно интересные области пространства состояний будут предпочитаться в процессе вычисления. Такая процедура называется неаналоговым вычислением Монте-Карло.
Метод Монте-Карло применим практически без ограничивающих условий. Тем не менее, он требует относительно больших вычислительных ресурсов, так как, например, 105 – 106 возможных историй жизни должны быть просчитаны по немалое число раз для достижения приемлемой статистической погрешности. Известными программами для решения задач переноса излучения по методу Монте-Карло являются, например, MORSE и MCNP.