3.3.1. Решения в простых частных случаях
При решении уравнения переноса излучения законченные аналитические выражения можно получить лишь для простых частных случаев. Ниже обсуждаются два примера, являющиеся особо важными для практического применения, несмотря на ограничивающие условия.
В первом примере описывается ослабление моноэнергетического фотонного излучения с энергией  бесконечным слоем толщиной
бесконечным слоем толщиной 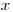 . Рассчитаем плотность потока фотонов, проходящих через слой без взаимодействия и регистрируемых детектором за защитой (рис. 3.7). Фотоны падают на защиту перпендикулярно параллельным пучком (коллимированный источник) и имеют плотность потока
. Рассчитаем плотность потока фотонов, проходящих через слой без взаимодействия и регистрируемых детектором за защитой (рис. 3.7). Фотоны падают на защиту перпендикулярно параллельным пучком (коллимированный источник) и имеют плотность потока 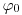 в точке
в точке 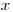 = 0. Поскольку в этом случае нет зависимости от энергии и направления, и экран не содержит источников, задача сводится к одномерному случаю, и уравнение радиационного переноса (3.46) упрощается:
= 0. Поскольку в этом случае нет зависимости от энергии и направления, и экран не содержит источников, задача сводится к одномерному случаю, и уравнение радиационного переноса (3.46) упрощается:
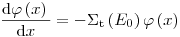 (3.48).
(3.48). Если толщина слоя 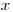 не слишком большая, и фотоны не могут рассеяться в начальное направление в результате многократного рассеяния, то интегрирование уравнения (3.48) дает решения уравнения переноса:
не слишком большая, и фотоны не могут рассеяться в начальное направление в результате многократного рассеяния, то интегрирование уравнения (3.48) дает решения уравнения переноса:
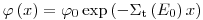 (3.49),
(3.49), т.е. оно соответствует экспоненциальному закону ослабления (см. также раздел 3.4.3). Граничным условием является то, что рассеянные фотоны не дают вклада в плотность потока 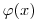 в точке детектора. Это условие может быть осуществлено экспериментально с помощью дополнительной коллимации детектора, как показано на рис. 3.7. Уравнение (3.49) является точным решением уравнения переноса излучения.
в точке детектора. Это условие может быть осуществлено экспериментально с помощью дополнительной коллимации детектора, как показано на рис. 3.7. Уравнение (3.49) является точным решением уравнения переноса излучения.
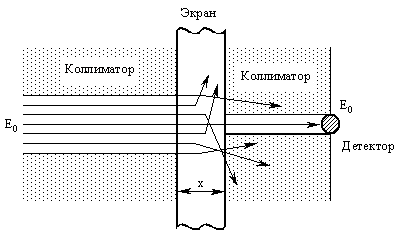
Рис. 3.7. Перенос фотонов через защиту в случае коллимации источника и детектора
Второй пример относится к замедлению нейтронов в бесконечной непоглощающей среде без источников. При таких условиях можно определить спектральную плотность потока 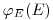 нейтронов. При преобразовании уравнения переноса важно отметить отсутствие пространственной или угловой зависимости и то, что полное сечение взаимодействия равно сечению рассеяния. Поэтому из уравнения (3.46) следует
нейтронов. При преобразовании уравнения переноса важно отметить отсутствие пространственной или угловой зависимости и то, что полное сечение взаимодействия равно сечению рассеяния. Поэтому из уравнения (3.46) следует
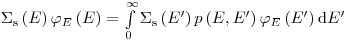 (3.50).
(3.50). Если рассеивающей средой является водород, то плотность вероятности имеет вид
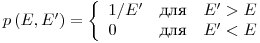 (3.51).
(3.51). Кроме того, сечение рассеяния 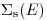 для водорода можно приблизительно считать независящим от энергии в диапазоне от 1 эВ до 1 МэВ. Отсюда следует
для водорода можно приблизительно считать независящим от энергии в диапазоне от 1 эВ до 1 МэВ. Отсюда следует
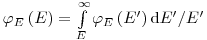 (3.52).
(3.52). Дифференцирование по нижнему пределу интегрирования 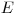 дает
дает
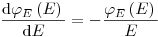 (3.53).
(3.53). Отсюда получается решение
 (3.54)
(3.54)или
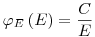 (3.55),
(3.55), где 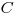 – константа. Уравнение (3.55) представляет собой спектр
– константа. Уравнение (3.55) представляет собой спектр 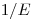 Ферми промежуточных нейтронов в водородосодержащих замедлителях (см. также раздел 3.4.2). Этот результат также является точным решением уравнения переноса при выше определенных условиях.
Ферми промежуточных нейтронов в водородосодержащих замедлителях (см. также раздел 3.4.2). Этот результат также является точным решением уравнения переноса при выше определенных условиях.