3.2. Уравнение переноса излучения

Для определения характеристик поля излучения в веществе или количества переданной энергии необходимо исследовать перенос излучения от источника, его поглощение или рассеяние в соответствующем элементе объема, в то же время принимая во внимание процессы взаимодействия, происходящие в веществе. Весь этот процесс переноса называется переносом излучения. При переносе частиц или фотонов происходит постоянное изменение их энергии и направления. 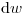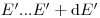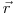Математическое описание этого процесса требует знания вероятности того, что ионизирующая частица с энергией в интервале и направлением движения после взаимодействия в точке будет иметь энергию 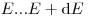и вылетит в направлении 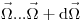. Эта вероятность может быть выражена через плотность вероятности :

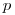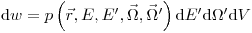(3.33),

где 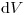– элемент объема в точке 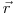. Перенос излучения можно промоделировать, разбив 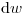на две независимые части:

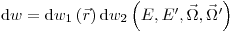(3.34).

Первая часть – это вероятность того, что взаимодействие произойдет в точке 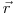, независимо от вида взаимодействия или изменения свойств вовлеченных в него частиц. Используя полное микроскопическое сечение 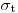для суммы всех возможных процессов взаимодействия:

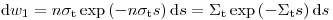(3.35).

Здесь 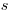– длина свободного пробега ионизирующей частицы до точки взаимодействия, 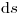– участок пути, на котором происходит взаимодействие, 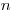– плотность частиц вещества, с которыми происходит взаимодействие. Величина

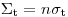(3.36)

представляет собой полное макроскопическое сечение взаимодействия, имеющее размерность обратной длины и связанное со средней длиной свободного пробега 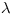выражением

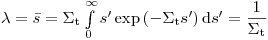(3.37).

Уравнение (3.35) справедливо в одномерном случае. Аналогичное соотношение можно записать для трехмерного случая (с началом координат в точке ):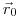

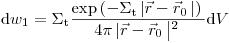(3.38).

Вторая часть уравнения (3.34) есть вероятность того, что в результате взаимодействия происходит изменение энергии и направления с 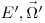на 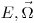. Для определения 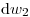необходима информация о виде взаимодействия. Использование соответствующего дифференциального сечения дает

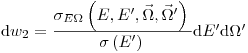(3.39).

С помощью соотношений (3.35) или (3.38) и (3.39) можно определить плотность вероятности .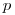

Перенос излучения можно описать математически с помощью уравнения переноса Больцмана, решение которого дает энергетическо-угловое распределение плотности потока 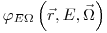в каждой точке 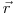для стационарного случая (т.е. пренебрегая временными зависимостями). Вывод уравнения переноса основан на составлении баланса для изменения плотности потока 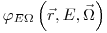со временем в элементарном объеме 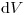, вызванного следующими процессами:

(1) Поглощение и рассеяние ионизирующих частиц с их выходом из рассматриваемых интервалов по энергии и направлению, задаваемое как

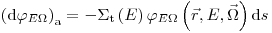(3.40).

(2) Рассеяние частиц из интервала энергий 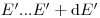и направлений в рассматриваемый интервал, задаваемое как

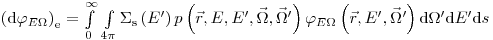(3.41),

где 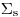– макроскопическое сечение рассеяния.

(3) Испускание источниками частиц с энергией и направлением, лежащими в рассматриваемых интервалах, задаваемое как

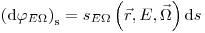(3.42),

где 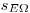– энергетическо-угловая плотность распределения источников.

В уравнениях (3.40) – (3.42) 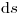описывает пробег частицы за время 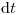в элементе объема 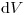. Полное изменение 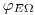в элементе объема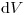

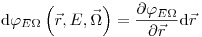(3.43),

так как

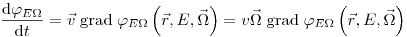(3.44).

Здесь 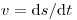– скорость частицы. Уравнение баланса

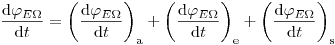(3.45)

после подстановки выражений (3.40) – (3.42) дает уравнение переноса Больцмана

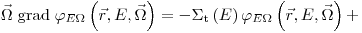(3.46)

.

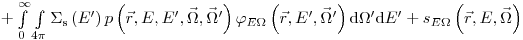Равенство (3.46) является интегро-дифференциальным уравнением, не имеющим решения в общем виде (в разделе 3.3 обсуждаются методы решения).

Кроме выведенной дифференциальной формы уравнения переноса часто используется интегральная форма, получаемая из математического преобразования соотношения (3.46). Для стационарного случая вводится вектор состояния 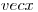шестимерного фазового объема 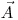, компонентами которого являются три пространственные координаты, две координаты направления и энергия частицы. Таким образом, зависимость от 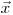означает зависимость от 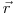, 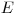и 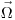. Тогда интегральная форма уравнения переноса имеет следующий вид:

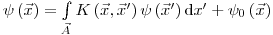(3.47).

Здесь 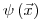– функция плотности распределения всех состояний частицы немедленно после взаимодействия, а 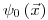– соответствующая функция сразу после образования частицы в источнике поля излучения. Величина 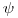может иметь различный физический смысл. Она может представлять собой распределение плотности потока 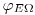по энергиям и направлениям, но может также относится к столкновениям или плотности энергетических потерь (см. раздел 3.4.2). Подынтегральная функция 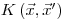в уравнении (3.47) описывает плотность вероятности перехода частицы в результате взаимодействия из состояния 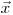в состояние 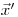. Уравнение переноса в интегральной форме (интегральное уравнение Фредгольма) также не имеет решения в общем виде.