Кривые самоослабления для препаратов с одинаковыми значениями общей активности

Другой метод определения коэффициента самоослабления — метод неактивной примеси – предполагает постоянство общей активности измеряемых образцов при различной их толщине. Массовая удельная активность препаратов в этом случае изменяется. Например, изготовлена серия препаратов осаждением из растворов с одинаковым количеством радионуклида, но различным количеством носителя. Результаты измерения этих образцов изображают в виде графика с толщиной образца по оси абсцисс и скоростью счета по оси ординат. Скорость счета бесконечно тонкого источника находят экстраполяцией кривой самоослабления к нулевой толщине препарата. Коэффициент самоослабления определяют как отношение скорости счета препарата данной толщины к скорости счета бесконечно тонкого образца (рис. 3.27). Метод дает точные результаты, если исходный радионуклид точно высокую удельную активность, что позволяет приготовить первый препарат бесконечно тонким.

Рис. 3.27. Кривая самоослабления при постоянной общей активности образцов (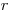 — толщина препаратов)

Максимум кривой при толщине препарата, равной 0,03 – 0,1 максимального пробега β-частиц используемого радионуклида, объясняется рассеянием β-частиц в материале самого препарата. В результате рассеяния изотропность углового распределения β-частиц нарушается, увеличивается число частиц, вылетающих под большим углом к плоскости препарата и попадающих в счетчик. При небольшой относительной толщине препарата увеличение скорости счета, обусловленное саморассеянием, может превысить эффект самопоглощения и привести к возрастанию регистрируемой активности. По достижении максимума скорость счета убывает с увеличением количества носителя примерно по экспоненциальному закону. При увеличении геометрического коэффициента максимум на экспериментальной кривой сглаживается и при значениях h, близких к 0,5, исчезает.

Получим выражение для приближенного расчета коэффициента самоослабления 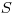при разбавлении радиоактивного образца неактивной примесью. Рассмотрим образец площадью 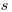и толщиной 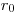(г/см²) с удельной активностью (в единицах регистрируемой активности) 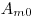. Пусть этот образец разбавляется неактивным материалом таким образом, что площадь его не изменяется, а толщина и удельная активность принимают соответственно значения 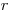и 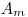(рис. 3.28). Очевидно, что при этом

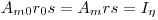(3.59),

,

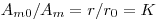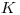представляет собой кратность разбавления.

Рис. 3.28. К расчету коэффициента ослабления при постоянной общей активности образцов

Определим число частиц 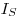, испускаемых с поверхности разбавленного образца, которое обусловлено элементом толщины : .

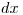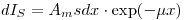Интегрируя это уравнение, находим:

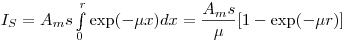(3.60).

Подставляя сюда 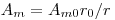и вводя кратность разбавления 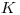, получаем:

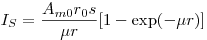(3.61);

.

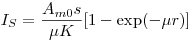Последнее соотношение позволяет оценить значение 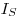на основании исходной удельной активности и известной кратности разбавления.

Из зависимости (3.61) с учетом (3.59) следует выражение для коэффициента самоослабления, совпадающее с (3.56). Это естественно, так как различные экспериментальные способы определения 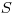должны в принципе приводить к одинаковым значениям. Нужно, однако, подчеркнуть, что область применения формулы (3.56) ограничивается большими значениями .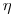