Кривые самоослабления для препаратов с одинаковой удельной активностью

Пусть массовая удельная активность используемых препаратов (число распадов в единицу времени на единицу массы вещества) постоянна, а их толщина 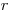изменяется. Например, приготовлено несколько образцов, полученных осаждением из кратных объемов радиоактивного раствора, причем все образцы имеют одинаковую площадь и радиоактивные атомы равномерно распределены в веществе каждого препарата. Очевидно, что при нулевой толщине препарата, т.е. при отсутствии радиоактивного вещества, скорость счета также равна нулю ( 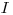= 0), а при некоторой предельной толщине препарата, отвечающей полному поглощению β-частиц с нижних слоев, скорость счета достигает насыщения (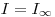). Этому случаю соответствует кривая 1 на рис. 3.25.

Число частиц, испускаемых в слое вещества препарата в телесный угол 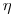, выражается прямой 2, проведенной из начала координат. Из-за саморассеяния излучения при малой толщине препаратов кривая 1 на начальном участке идет выше прямой 2. Точно определить наклон прямой 2 трудно. На практике ее заменяют касательной 3, проходящей через начало координат.

На начальном участке кривая самоослабления сливается с касательной, следовательно, для достаточно тонких препаратов потери излучения в слое радиоактивного вещества практически отсутствуют. Для образцов, толщина которых меньше слоя насыщения, но уже обусловливает поглощение β-излучения, поправочный коэффициент 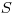определяется как отношение ординат касательной и кривой самоослабления при некоторой определенной толщине слоя препарата.

На рис. 3.26 показана кривая самоослабления для образцов ВаСO₃ (использовали торцовый счетчик со слюдяным окном толщиной 3 мг/см² и диаметром 60 мм; препараты, нанесенные на алюминиевые диски, размещали в двух миллиметрах от окна счетчика).

Обычно рекомендуется вести работу с достаточно тонкими образцами, для которых можно пренебречь эффектом самоослабления, или с «бесконечно толстыми» образцами (слой насыщения), для которых регистрируемая активность пропорциональна удельной активности. Минимальная толщина образца, отвечающая слою насыщения, не превышает максимального пробега β-излучения в материале препарата, а для большинства практических целей, благодаря весьма незначительному влиянию нижних слоев и дополнительному поглощению в окошке счетчика, достаточна толщина 0,75.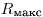

Иногда необходимо привести скорость счета препарата толщиной 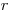к скорости счета «бесконечно толстого» слоя. На основании выражений (3.54) и (3.56) имеем:

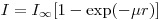(3.58).

Чтобы получить более точные значения скорости счета, приведенной к слою насыщения, необходимо пользоваться градуировочной кривой, построенной для серии препаратов, приготовленных из того вещества, в форме которого радионуклид поступает на измерение в данной работе.