Расчет для точечного источника при осевом расположении

Рис. 3.6. К расчету геометрического коэффициента для торцового счетчика без диафрагмы (а) и с диафрагмой (б) (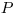 — измеряемый образец)

Рассмотрим точечный источник, расположенный на продолжении оси торцового счетчика. Пусть 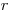— радиус окна счетчика (рис. 3.6,a), а 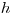— расстояние от препарата до окна счетчика. Телесный угол 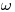, под которым счетчик облучается источником излучения, равен:

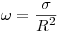(3.23),

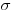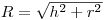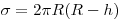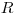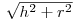где – поверхность шарового сегмента радиусом . Принимая во внимание, что , и заменяя на , получаем:

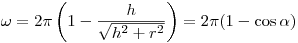(3.24),

где 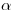— апертура угла, под которым чувствительный объем счетчика виден из препарата, причем .

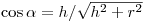Подставив найденное значение в формулу (3.24), окончательно получим:

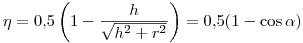(3.25).

Если на максимально близком расстоянии от окна счетчика установить диафрагму, диаметр которой в 1,5-2 раза меньше диаметра окна счетчика (см.рис. 3.6,б), то по-прежнему будет выражаться формулой (3.25), но 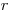будет соответствовать радиусу отверстия диафрагмы, а 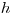— расстоянии от препарата до верхней плоскости диафрагмы. Диафрагмы изготовляют обычно из листа алюминия или латуни толщиной не менее слоя полного поглощения β-частиц исследуемого излучения; края диафрагмы делают скошенными по направлению крайних лучей от препарата. Применение диафрагм позволяет точнее фиксировать относительный телесный угол, особенно если неизвестно точное положение чувствительного объема счетчика. Одновременно улучшается воспроизводимость показаний прибора.

Таблица 3.4

Значения геометрического коэффициента 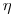при различных расстояниях от торцового счетчика до точечного препарата, расположенного по его оси

0,05

0,475

0,40

0,314

1,2

0,116

4,0

0,0149

0,10

0,450

0,50

0,276

1,4

0,093

4,5

0,0118

0,15

0,426

0,60

0,243

1,6

0,076

5,0

0,0097

0,20

0,402

0,70

0,213

1,8

0,063

6,0

0,0068

0,25

0,379

0,80

0,188

2,0

0,053

7,0

0,0050

0,30

0,356

0,90

0,165

2,5

0,036

8,0

0,0038

0,35

0,335

1,00

0,146

3,0

0,026

9,0

0,0030

3,5

0,019

10,0

0,0025

Как видно из табл. 3.4, значения 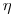при малых 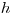сильно изменяются в результате небольших вертикальных смещений препарата относительно счетчика. При малых расстояниях между источником и счетчиком значение телесного угла сильно зависит даже от небольших изменений этого расстояния. Так, для того чтобы погрешность определения телесного угла не превышала 0,5%, источник необходимо установить с отклонением не более ±0,04 мм. при расстоянии между источником и счетчиком от 5 до 10 мм.; ±0,1 мм — при расстоянии 5 см. Очевидно, что обеспечение такой высокой точности установки источника практически неосуществимо, если учесть, что измеряемый источник обычно бывает нанесен на подложку из тонкой пленки, которая может прогибаться в ту или другую сторону. Менее точная установка источника допустима при больших расстояниях между источником и счетчиком, однако увеличение этого расстояния невыгодно из-за сильного уменьшения скорости счета вследствие уменьшения телесного угла.

Чтобы улучшить воспроизводимость геометрических условий измерения, следует располагать препарат возможно дальше от счетчика. Однако с увеличением расстояния возрастает поглощение и рассеяние в воздухе β-излучения низкой энергии, а из-за уменьшения телесного угла падает скорость счета. Поэтому целесообразно помещать препарат в среднем на расстоянии 3–4 см от окошка счетчика с диаметром входного окна 20 мм (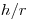 =3 ÷ 4).