Определение разрешающего времени

Из выражения (3.8) следует, что

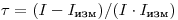(3.12).

Это соотношение позволяет определить разрешающее время, если известно полное число частиц 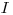, попадающих в счетчик в единицу времени, и измеренная прибором скорость счета 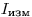. Для определения 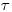измеряют скорость счета серии специально изготовленных стандартных препаратов с известным количеством радионуклида. (Вообще говоря, достаточно иметь серию препаратов различной активности, приготовленных из известных объемов исходного радиоактивного раствора). На графике (рис. 3.4) при малых скоростях счета, когда поправка на разрешающее время ничтожно мала, получается прямая. При дальнейшем увеличении активности препаратов наблюдается отступление от линейности. Экстраполируя начальный участок кривой, можно для каждой измеренной скорости счета 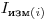определить полное число попавших в счетчик частиц .

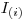Рис. 3.4. Определение поправки на разрешающее время методом серии препаратов

Рис. 3.5. Определение поправки на разрешающее время методом кривой распада короткоживущего нуклида

Для определения поправки на разрешающее время не обязательно иметь серию стандартных препаратов; можно воспользоваться каким-либо короткоживущим радионуклидом (например, ¹²⁸I с периодом полураспада 25 мин). Свежеприготовленный препарат йода помещают в измерительный домик и проводят систематические наблюдения скорости счета через определенные интервалы времени (обычно через 5-10 мин). Когда радионуклид достаточно распадется, регистрируемое число импульсов будет соответствовать числу попавших в счетчик частиц.

Без построения градуировочной кривой можно определить разрешающее время методом двух препаратов

.

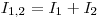Распишем данное выражение в виде

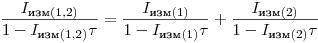(3.13).

При выводе формулы для определения 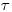по данным измерения двух препаратов возможны различные подходы. Если выполняется условие 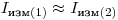, то в знаменателях в правой части равенства (3.13) вместо этих величин можно, подставить 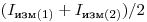. В результате получится уравнение

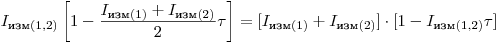(3.14),

откуда

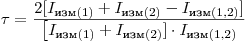(3.15).

Принимая во внимание, что 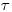мало, можно пренебречь в уравнении (3.13) членами, содержащими :

,

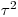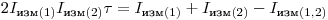откуда

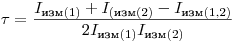(3.16).

Выражение (3.8) можно представить в виде бинома .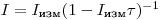

Если в разложении бинома ограничиться двумя первыми членами, то получится приближенное соотношение 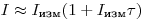. Тогда на основании (3.13) можно записать:

,

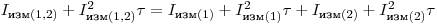и, таким образом,

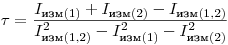(3.17).

Более точную формулу для расчета 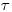можно получить, не пренебрегая в выражении (3.13) членами, содержащими 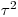, а решая соответствующее квадратное уравнение. Равенство (3.13) преобразуется к виду

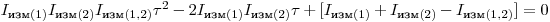(3.18).

Решение этого уравнения может быть записано как

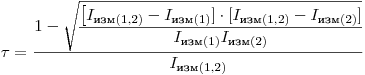(3.19).