Разрешающее время продлевающегося типа

Характерная особенность разрешающего времени продлевающегося типа: каждое попадание частицы в счетчик за время 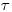после очередного отсчета продлевает разрешающее время еще на интервал 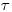. Обозначим среднее число частиц, попадающих в счетчик в единицу времени, 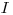, а среднее число частиц, измеряемое прибором за единицу времени, 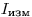. 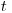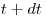Чтобы установка зарегистрировала частицу, попавшую в счетчик в интервал времени от до , необходимо, чтобы за время от 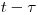до 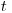через счетчик не прошла ни одна частица. Вероятность того, что ни одна частица не попадет в счетчик за время 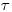(иными словами, вероятность того, что частица, попавшая в счетчик за последующий интервал времени 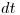,будет зарегистрирована), равна 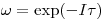. Тогда число частиц, измеренное прибором за время 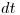, 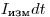будет равно произведению 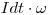, т.е.

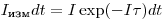(3.1).

Следовательно, общее число частиц, измеренное прибором в единицу времени,

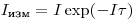(3.2).

Формулу (3.2) можно представить также в виде

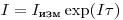(3.3).

Определим максимальное значение скорости счета 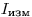в зависимости от 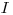, для чего возьмем соответствующую производную:

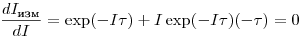(3.4) ;
.

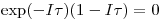Поскольку вероятность 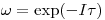отлична от нуля, приравниваем к нулю множитель в скобках: . Отсюда можно найти значение 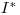, при котором 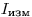достигает максимума:

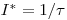(3.4).

Подставляя 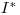вместо 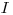в формулу (3.2), получаем:

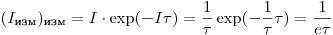(3.5),

и, следовательно,

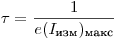(3.6).

Найденное выражение указывает простой экспериментальный способ определения 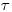. Следует взять достаточно сильный источник излучения и приближать его к счетчику до тех пор, пока число сосчитываемых в единицу времени импульсов не достигнет наибольшего значения. Дальнейшее приближение источника излучения будет вызывать уменьшение числа сосчитанных импульсов. (Экстремальный характер зависимости измеряемой активности от числа попадающих в счетчик частиц как раз и является признаком разрешающего времени продлевающегося типа): Подставляя значение 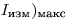в формулу (3.6), рассчитывают 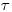. Конечно, такой метод связан с перегрузкой аппаратуры и потому в некоторых случаях применение его может оказаться нежелательным.

После несложных преобразований формула (3.3) приобретает более удобный для практических расчетов вид [6]. Логарифмируя выражение (3.3) и умножая обе части полученного выражения на 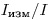получаем:

,

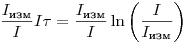или

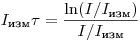(3.7).

Последнее выражение позволяет рассчитать 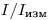как функцию экспериментально измеренной величины 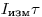. Эта зависимость приведена в табл. 3.1 и на рис. 3.2.

Таблица 3.1

Зависимость между поправкой на разрешающее время 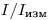и значением произведения 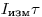, рассчитанная по формуле (3.7)

1,01

0,010

1,17

0,134

2,5

0,367

1,02

0,019

1,18

0,140

2,6

0,368

1,03

0,029

1,19

0,146

2,7

0,368

1,04

0,038

1,2

0,152

2,8

0,368

1,05

0,047

1,3

0,202

2,9

0,367

1,06

0,055

1,4

0,240

3,0

0,366

1,07

0,063

1,5

0,270

3,1

0,365

1,08

0,071

1,6

0,294

3,2

0,364

1,09

0,079

1,7

0,312

3,3

0,362

1,10

0,087

1,8

0,327

3,4

0,360

1,11

0,094

1,9

0,338

3,5

0,358

1,12

0,101

2,0

0,347

3,6

0,356

1,13

0,108

2,1

0,353

3,7

0,354

1,14

0,115

2,2

0,358

3,8

0,351

1,15

0,122

2,3

0,362

3,9

0,349

1,16

0,128

2,4

0,365

4,0

0,347

Рис. 3.2. Зависимость между поправкой на разрешающее время 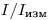и значением произведения 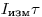, рассчитанная по формуле (3.7)

Графиком, представленным на рис. 3.2, можно пользоваться для определения полного числа частиц 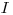, попавших в счетчик в единицу времени (скорости счета, исправленной на разрешающее время). Для этого умножают измеренную прибором скорость счета 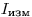препарата на разрешающее время 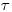и из графика определяют 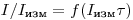. Для достаточно больших произведений 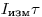каждому значению ординаты на рис. 3.2 соответствуют две точки на абсциссе. Чтобы установить, какое из значений 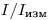соответствует действительности, достаточно несколько удалить препарат от счетчика. Если при этом 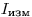уменьшится, то отношение 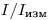следует брать слева от максимума кривой; если же 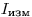увеличится, то значение 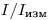следует искать справа от максимума.