6.6. Определение эффективности фильтра при измерении альфа-активных аэрозолей
Задержка аэрозолей на фильтре при протягивании воздуха происходит не только в верхних слоях его, но и в слоях более глубоких. Так как пробег α-частиц в материале фильтра сравним с толщиной фильтра, то необходимо вводить поправку на поглощение α-частиц в нем.
Пусть имеется тонкий α-источник, испускающий 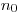 α-частиц в единицу времени в направлении 2π. Если накрыть его тонким листом поглотителя, то количество α-частиц
α-частиц в единицу времени в направлении 2π. Если накрыть его тонким листом поглотителя, то количество α-частиц 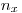 , прошедших через поглотитель, определяется по соотношению, имеющему следующий вид:
, прошедших через поглотитель, определяется по соотношению, имеющему следующий вид:
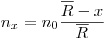 (6.3),
(6.3), где 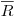 – средний пробег α-частиц в поглотителе;
– средний пробег α-частиц в поглотителе; 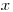 – толщина поглотителя.
– толщина поглотителя.
Зависимость счета эталонного α-источника на установке от толщины поглотителя для большинства установок представляет собой прямую линию (рис. 5.10) и может быть записана в таком виде:
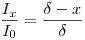 (6.4).
(6.4).
Рис. 6.8. Кривая зависимости скорости счета α-частиц от толщины фильтра Петрянова на сцинтилляционной приставке
Величина 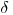 представляет собой минимальную толщину слоя фильтра свыше которой α-частицы практически не регистрируются. Она зависит от эффективности счета установки и всегда меньше пробега α-частиц в материале фильтра. На практике величину
представляет собой минимальную толщину слоя фильтра свыше которой α-частицы практически не регистрируются. Она зависит от эффективности счета установки и всегда меньше пробега α-частиц в материале фильтра. На практике величину 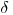 можно определить по уравнению (6.4) по нескольким замерам эталонного источника без поглотителя и с поглотителем. Расчет ведется по формуле:
можно определить по уравнению (6.4) по нескольким замерам эталонного источника без поглотителя и с поглотителем. Расчет ведется по формуле:
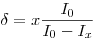 (6.5).
(6.5). Для определения эффективности фильтра необходимо знать не только закон поглощения α-частиц в фильтре, но и распределение активныых аэрозолей в фильтре и проскок аэрозолей через фильтр. Распределение аэрозолей в фильтре зависит от дисперсности аэрозолей, скорости протягивания воздуха, толщины, волокон фильтра и его плотности, заряда пылинок и других факторов. Для монодисперсных аэрозолей и фильтра, имеющего равномерную плотность, фильтрация аэрозолей подчиняется экспоненциальному закону:
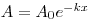 (6.6),
(6.6), где 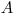 —активность аэрозолей, прошедших через слой фильтра толщиной
—активность аэрозолей, прошедших через слой фильтра толщиной 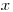 , мг/см2;
, мг/см2; 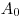 — полная активность аэрозолей в прокачанном воздухе;
— полная активность аэрозолей в прокачанном воздухе; 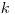 — коэффициент, характеризующий фильтрующую способность фильтра, см2/мг.
— коэффициент, характеризующий фильтрующую способность фильтра, см2/мг.
Согласно уравнению (6.6), количество активной аэрозолей, осажденной в элементарном слое фильтра 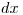 на глубине
на глубине 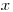 , будет определяться по соотношению, имеющему следующий вид:
, будет определяться по соотношению, имеющему следующий вид:
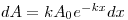 (6.7).
(6.7). Под коэффициентом проскока 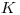 понимается отношение количества активной аэрозолей, прошедшей через фильтр толщиной
понимается отношение количества активной аэрозолей, прошедшей через фильтр толщиной 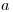 , к количеству активной аэрозолей, содержавшейся в прокачанном воздухе, т.е.
, к количеству активной аэрозолей, содержавшейся в прокачанном воздухе, т.е.
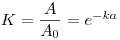 (6.8).
(6.8). Так как распределение аэрозолей в фильтрах при стандартных условиях аспирации одно и то же, то при прокачке воздуха через два фильтра проскок 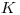 может быть определен по соотношению:
может быть определен по соотношению:
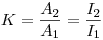 (6.9),
(6.9), где 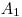 — активность аэрозолей на первом фильтре;
— активность аэрозолей на первом фильтре; 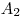 — активность аэрозолей на втором фильтре;
— активность аэрозолей на втором фильтре; 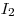 ,
, 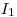 – количество импульсов на радиометрической установке при измерении второго и первого фильтров.
– количество импульсов на радиометрической установке при измерении второго и первого фильтров.
Проскок 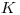 необходимо определять для каждой серии замеров загрязненности воздуха радиоактивной пылью.
необходимо определять для каждой серии замеров загрязненности воздуха радиоактивной пылью.
На практике обычно встречаются аэрозоли, имеющие различную дисперсность. В этом случае экспоненциальный закон фильтрации выполняется лишь приблизительно. Однако для дозиметрических замеров можно принять экспоненциальный закон фильтрации.
Для более точных измерений определяют распределение аэрозолей в фильтре экспериментально. Для этой цели воздух протягивается через 10 тонких фильтров. После измерения фильтров графическим путем определяется эффективность фильтра.
Зная распределение активной аэрозолей в фильтре и закон поглощения α-частиц в материале фильтра, выведем формулу эффективности фильтра.
Для этого предположим, что эффективность счета установки равна 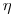 (по отношению к углу 4π). Тогда соотношение между скоростью счета установки и активностью
(по отношению к углу 4π). Тогда соотношение между скоростью счета установки и активностью 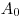 , содержавшейся в прокачанном воздухе, исходя из уравнений (6.3) и (6.8), можно записать в виде:
, содержавшейся в прокачанном воздухе, исходя из уравнений (6.3) и (6.8), можно записать в виде:
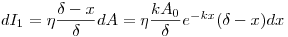 (6.10).
(6.10). В случае 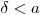 , где
, где 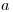 — толщина фильтра,
— толщина фильтра,
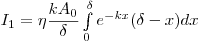 (6.11).
(6.11). Эффективность фильтра 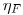 , по определению, есть отношение
, по определению, есть отношение
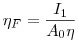 (6.12).
(6.12). Тогда из уравнений (6.10) и (6.11) эффективность фильтра определяется по соотношению:
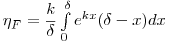 (6.13),
(6.13), после решения которого получим:
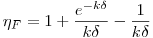 (6.14).
(6.14). Из уравнения (6.8) находим:
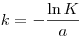 (6.15).
(6.15). Следовательно, эффективность фильтра в случае 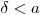 может быть определена по формуле:
может быть определена по формуле:
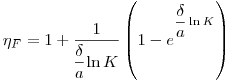 (6.16).
(6.16). Таким же образом получена формула эффективности фильтра 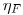 в случае
в случае 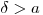 . Она имеет вид:
. Она имеет вид:
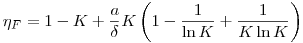 (6.17).
(6.17). В случае 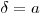 эффективность фильтра определяется по формуле:
эффективность фильтра определяется по формуле:
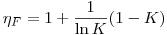 (6.18).
(6.18).