4.4. Зонды Брэгга—Грея

Другой важный принцип дозиметрии воплощен в определении поглощенной дозы излучения при помощи зондов Брэгга—Грея. В отличие от равновесных зонды Брэгга—Грея могут применяться в первичных радиа­ционных полях как незаряженных, так и заряженных частиц. Эти зонды можно применять в первичных ра­диационных полях незаряженных частиц независимо от того, осуществляется ли равновесие вторичных частиц. Зонд удовлетворяет условиям Брэгга—Грея, если:

а) поток, энергетический спектр и распределение по направлениям заряженных частиц внутри зонда прост­ранственно постоянны и равны потоку, энергетиче­скому спектру и распределению по направлениям в месте измерения в облучаемом материале (при отсут­ствии зонда);

б) заряженные частицы, высвобожденные косвенно ионизирующими частицами в зонде, вносят пренебре­жимо малый вклад в дозу излучения, поглощенную в зонде.

Условия Брэгга—Грея в принципе выполнимы только приближенно. Линейные размеры зонда, в котором поток, распределение по направлениям и энергетиче­ский спектр заряженных частиц заметно не изменя­ются (см. условие «а»), должны быть малы по срав­нению со средней длиной пробега 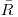заряженных час­тиц (например, 0,1).

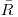Из условия «б» вытекает требование, чтобы размеры зонда были малы по сравнению с длиной ослабления 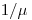( 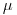— линейный коэффициент ослабления), т. е. средним свободным пробегом незаряженных частиц. Однако определяющим для измерительного объема зонда Брэгга—Грея все же является значение .

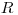Перенос энергии на измерительный объем зонда Брэгга—Грея обусловлен исключительно заряжен­ными частицами. Потери энергии заряженных частиц при прохождении через материал можно описать с по­мощью массовой тормозной способности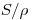, которая определяется следующим образом:

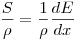(4.18),

где 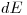есть средняя потеря в энергии заряженной час­тицы с энергией 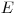вдоль элемента пути 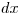в мате­риале плотности .

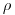Потери в энергии заряженных частиц происходят главным образом путем ионизационного торможения в результате столкновений с оболочечными электро­нами и путем излучательного торможения. Определя­ющей величиной в передаче энергии материалу/в эле­менте его объема (а также в зонде Брэгга—Грея) яв­ляется доля 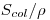массовой тормозной способности, обусловленная столкновениями. Энергия, переданная фотонам при излучательном торможении, большей частью выносится из того элемента объема, в котором возникло тормозное излучение.

Теория Брэгга—Грея исходит из приближения, со­гласно которому энергия, отданная при столкновениях с электронами атомов вследствие их ионизации и воз­буждения, полностью остается в элементе объема. Та­ким образом, энергия заряженных частиц постепенно убывает вдоль элемента пути 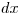, в какой-то мере по­глощаясь «на месте». Тогда между поглощенной дозой излучения 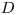и флюенсом 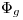моноэнергетических заря­женных частиц энергии 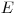существует соотношение

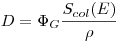(4.19).

С помощью этого основополагающего соотношения можно рассчитать чувствительность зонда Брэгга— Грея. Отношение дозы излучения 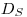, поглощенной в зонде, к дозе, поглощенной в облученном материале, можно вычислить, исходя из формулы (3.19), при по­мощи уравнения Брэгга—Грея:

(4.20).

Отношение массовых тормозных способностей называется относительной тормозной способностью.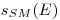

Чувствительность 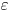зонда Брэгга—Грея для моно­энергетических заряженных частиц получается умно­жением отношения массовых тормозных способностей зондового вещества 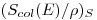и облученного мате­риала 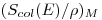на собственную чувствительность 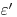, которая для одного вида частиц постоянна у боль­шинства измерительных материалов:

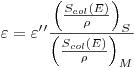(4.21).

В своей первоначальной форме теория Брэгга—Грея рассматривает отношение массовых тормозных спо­собностей материалов с различными порядковыми но­мерами как независимое от энергии 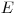заряженных, частиц, хотя сами массовые тормозные способности; сильно зависят от энергии. В действительности для от­ношения массовых тормозных способностей имеет место некоторая энергетическая зависимость, которая тем более ярко выражена, чем сильнее различаются эффективные порядковые номера зондового вещества и облученного материала. Относительная чувствительность 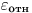зонда Брэгга—Грея определяется аналогично выражению (4.16) следующим образом:

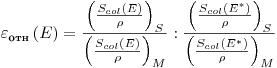(4.22).

На рис. 4.6 показана зависимость 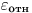для зондов Брэгга—Грея из ПММА и LiF от энергии электрон­ного излучения (облучаемый материал — мускульная; ткань; выбранная энергия отсчета 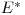= l МэВ). Из графиков видно, что обусловленная этой зависимостью погрешность определения поглощенной дозы излуче­ния в фотонных и электронных радиационных полях, с неизвестными энергетическими спектрами (в диапа­зоне энергий от 0,1 до 100 МэВ) не превышает не­скольких процентов, независимо от того, при какой энергии проводилась калибровка зонда.

Для точного определения чувствительности зонда Брэгга—Грея необходимо знать спектральное распре­деление энергии заряженных частиц в точке измере­ния. Учитывая функцию распределения энергии 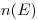и исходя из формулы (4.18), получаем для отношения 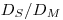следующее выражение:

(4.23),

где 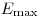есть максимальная энергия в энергетическом: спектре заряженных частиц. Величина 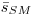называется: эффективным отношением массовых тормозных спо­собностей. В силу того, что передача энергии вдоль элемента пути 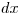предполагается непрерывной, соот­ношение (4.23) является приближенным.

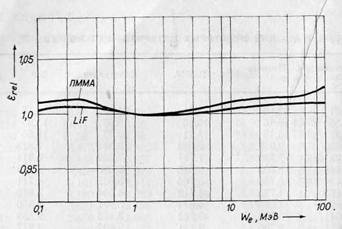
Рис. 4.6. Относительная чувствительность 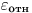зондов Брэгга—Грея из LiF и ПММА по отношению к мускульной ткани в зависимости от энергии электронов

Теория Брэгга—Грея была в дальнейшем успешно усовершенствована преимущественно для дозиметрии радиационных полей γ-излучения Спенсером и Аттиксом. Они предположили, что заряженные час­тицы могут в столкновениях создавать δ-электроны, пробег которых сравним с пробегами соударяющихся частиц. Поэтому заряженные частицы теряют свою энергию дискретно. Из выражения (4.19), собственно говоря, и не вытекает, что энергия, переданная в столк­новениях, должна поглощаться «на месте». Требуется лишь соблюдение условий равновесия для электронов, высвобожденных в столкновениях. Однако равновесие осуществляется только для δ-электронов, пробеги ко­торых не намного больше, чем размеры зонда Брэгга— Грея. Поглощенная доза излучения, вычисленная по формуле (4.19), получается слишком высокой, ибо δ-электроны с большим пробегом, для которых не имеет место равновесие, выносят из рассматриваемого эле­мента объема больше энергии, чем в него поступает. Отличие фактической поглощенной дозы от расчетной компенсируется введением в формулу (4.23) ограни­ченной массовой тормозной способности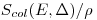 для зондового вещества облучаемого материала.

Эта модифицированная тормозная способность учи­тывает только процессы столкновения с потерями энергии до определенной максимальной энергии 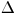. Кроме того, учитывается энергетический спектр 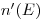вторичных электронов, измененный под действием δ-электронов с энергиями, превышающими 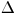. Интегрирование осуществляется только начиная со значения энергии 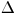. Таким образом, более точный расчет отношения 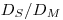, чем по формуле (4.23), приводит к следующему выражению:

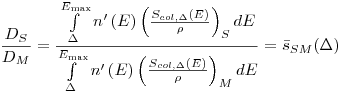(4.24).

Энергию 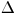выбирают таким образом, что средний про­бег δ-электронов с энергией 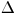примерно сравним с данными измерений при помощи зонда Брэгга—Грея. Выражение (4.23) не учитывает то обстоятельство, что равновесие δ-электронов с энергиями меньше 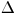нарушается в области измерений самим измерительным объемом. Доза излучения 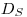, поглощенная зондом, лишь приближенно пространственно постоянна внутри него. Для эффективного отношения массовых тормоз­ных способностей, полученного по формуле (4.24), характерна зависимость от зондовых измерений, обусловленная выбором значения 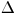. Варьирование изме­рений допустимо, однако, лишь в рамках выполнения условий Брэгга—Грея.

В противоположность уравнению Брэгга—Грея (4.20) соотношения (4.23) и (4.24) имеют лишь несущественное значение для практической дозиметрии. Их применение часто затрудняется тем, что энергетические спектры 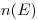или 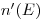бывают либо неизвестны, либо недостаточно известны. В самом неблагоприятном случае (облучаемый материал — свинец) разница между значениями, рассчитанными по формулам (4.23) и (4.24), меньше 20%. Для элементов с более низким порядковым номером эффективные отношения массовых тормозных способ­ностей, полученные без поправки на 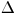, находятся в согласии с экспериментально полученными значениями 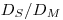(в пределах точности измерений 1—2%).

В качестве измерительного вещества в зондах Брэгга—Грея используется главным образом воздух. При нормальном давлении объем воздуха с линейными размерами менее 1 см отвечает условиям Брэгга—Грея для электронов с минималь­ной энергией порядка 0,1 МэВ. Поскольку при еще меньших объемах собственная чувствительность зонда становится слишком низкой, воздушные зонды Брэгга— Грея (полостные камеры) применяются в радиацион­ных полях γ-излучения и электронов лишь при пер­вичных энергиях, превышающих 0,1 МэВ. В случае твердотельных зондов условия Брэгга—Грея выполня­ются для энергий порядка 0,1 МэВ лишь со значитель­ными ограничениями. При плотности измерительного вещества 1 г/см^–3 линейные размеры зонда должны быть порядка 10 мкм. Условия Брэгга—Грея удается приближенно выполнить, используя тонкие зонды (например, антраценовые пленки, LiF в тефлоновой пленке) при преимущественно перпендикулярном па­дении частиц. Некоторые специальные измерительные задачи — например, дозиметрия в пограничном слое между материалами с различными порядковыми но­мерами — могут быть решены только при помощи зон­дов такого типа.

Для высокоэнергетического излучения нееобходимы более крупные измерительные объемы (линейные раз­меры в случае твердотельных зондов должны быть больше 0,1 мм). В фотонных радиационных полях, в которых при энергиях, превышающих 3 МэВ, равно­весие вторичных электронов уже неосуществимо, из­мерения поглощенной дозы излучения могут быть ос­нованы только на принципе Брэгга—Грея.