4.2. Равновесие вторичных частиц
Равновесие вторичных частиц является важнейшим частным случаем, допускающим дальнейшую разработку общих соотношений (2.22) и (2.23). При этом расчет чувствительности зондов (равновесных зондов) значительно упрощается. Кроме того, равновесие вторичных частиц играет решающую роль при измерении экспозиционной дозы излучения.
В радиационном поле в области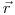 
имеет место равновесие вторичных частиц, если векторный поток энергии 
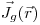вторичных заряженных частиц, образованных первичными частицами, удовлетворяет условию
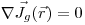(4.3). Уравнение (4.3) означает, что сумма кинетических энергий всех заряженных частиц, поступающих в элемент объема в области 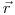, равна сумме кинетических энергий всех вторичных частиц, выходящих из этого элемента объема.
Равновесие вторичных частиц в области 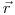осуществляется, если:
а) поток, энергетический спектр и распределение по направлениям первичных частиц
и
б) коэффициенты взаимодействия излучение—материал (массовый коэффициент поглощения энергии или массовая тормозная способность) для первичных и вторичных частиц
пространственно постоянны в области, из которой заряженные вторичные частицы могут попасть в элемент объема в область
Массовый коэффициент поглощения энергии (см. формулу (4.8)) и массовая тормозная способность зависят от атомного состава облучаемого материала. Массовая тормозная способность, кроме того, еще незначительно зависит от плотности материала (эффект плотности). Однако в практической дозиметрии этим влиянием в большинстве случаев можно пренебречь. Таким образом, равновесие вторичных частиц может иметь место в материалах с однородным атомным составом, но с пространственно зависимой плотностью (например, на границе раздела полиэтилен—этилен). Это положение основано на теореме, доказанной Фано:
Если в материале с однородным атомным составом поток, энергетический спектр и распределение по направлениям первичного излучения пространственно постоянны, то поток, энергетический спектр и распределение по направлениям вторичного излучения также постоянны и не зависят от плотности материала.
При однородной плотности облучаемого материала область пространства, характеризующаяся наличием условий для равновесия вторичных частиц, ограничивается шаровой поверхностью, причем радиус шара равняется максимальному пробегу вторичных частиц. Если в центре шара имеет место равновесие вторичных частиц, то число вторичных частиц, высвобожденных в каждом элементе объема, спектр начальных кинетических энергий и начальное распределение вторичных частиц по направлениям постоянны по меньшей мере в пределах объема шара.
Условие «а» для равновесия вторичных частиц полностью осуществимо лишь при равномерном распределении радиоактивного вещества в бесконечно протяженном материале. Однако если первичное излучение поступает в материал извне, то с увеличением глубины проникновения происходит большее или меньшее ослабление потока частиц. В общем случае изменяются также распределения первичных частиц по энергиям и направлениям. Равновесие вторичных частиц может реализоваться (в некотором приближении) только в том случае, если первичное радиационное поле изменяется лишь незначительно внутри области, размеры которой сравнимы с максимальным пробегом вторичных частиц. В дозиметрии можно говорить об осуществлении равновесия вторичных частиц, если длина ослабления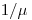 
(
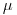— линейный коэффициент ослабления), т.е. длина максимального пробега первичных частиц, не менее чем в 10 раз превышает средний максимальный пробег вторичных частиц.
На рис. 4.2 представлены кривые зависимостей ослабления 
для γ-излучения и среднего массового пробега 
электронов в воде от энергии частиц. Как видно, до энергий около 3 МэВ массовая длина ослабления для моноэнергетических фотонов, определенная по , более чем в 10 раз превышает средний пробег электронов той же энергии, являющейся одновременно максимальной энергией вторичных электронов, порожденных γ-излучением.
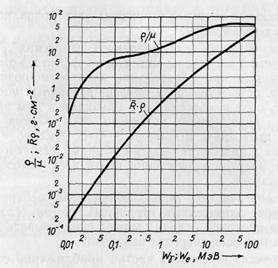
Рис. 4.2. Длина массового ослабления для γ-излучения и средний пробег электронов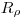 
в воде в зависимости от энергии
Таким образом, для фотонного излучения, освобождающего электроны путем фотоэффекта, комптон-эффекта или при образовании электронно-позитрон-ных пар, осуществимо равновесие вторичных частиц в воздухе, воде и материалах с близкими к ним эффективными порядковыми номерами, если энергия фотонов не превышает примерно 3 МэВ. Именно в этих пределах и находится энергия обычных рентгеновских лучей и энергии γ-излучения почти всех радиоактивных нуклидов.
В биологической ткани, облучаемой нейтронами, равновесие заряженных вторичных частиц (главным образом протонов отдачи) может существовать практически при всех энергиях нейтронов.
Равновесие вторичных частиц приближенно соблюдается также и в первичных электронных радиационных полях, в которых пробег высвобожденных в ионизационных процессах электронов (δ-электронов) ничтожно мал по сравнению с пробегом первичных электронов. Высокоэнергетические δ -электроны, максимальная энергия которых может достигать половины энергии ударяющего первичного электрона, нарушают равновесие (см. раздел 4.4).
В первичном радиационном поле незаряженных частиц (фотонов, нейтронов) при равновесии вторичных частиц имеем
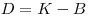(4.4). Пренебрегая потерями на тормозное излучение, получаем
(4.5). Энергия, переданная материалу в элементе объема, при наличии равновесия вторичных частиц равна сумме начальных кинетических энергий всех заряженных вторичных частиц, высвобожденных в этом объеме, хотя они в нем и не поглощаются полностью.
Передача энергии от незаряженных на заряженные частицы внутри элемента массы описывается массовым коэффициентом передачи энергии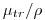 
, а для учета потерь на тормозное излучение 
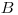делается поправка к массовому коэффициенту передачи энергии и вводится массовый коэффициент поглощения энергии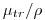. Дадим определения:
Линейный коэффициент ослабления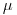 — отношение доли 
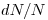фотонов данной энергии, претерпевших взаимодействие при прохождении элементарного пути 
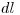в среде, к длине этого пути:
(4.6). Линейный коэффициент передачи энергии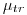
— отношение доли энергии 
падающего γ-излучения, которая превращается в кинетическую энергию электронов при прохождении элементарного пути 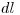в среде, к длине этого пути
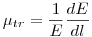(4.7). Линейный коэффициент поглощения энергии
— разность между линейным коэффициентом передачи энергии 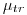и произведением этого коэффициента 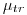на долю 
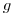энергии вторичных электронов, переходящей в тормозное излучение в данном веществе:
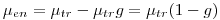(4.8). Массовые коэффициента взаимодействия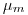
— отношение соответствующих линейных коэффициентов взаимодействия к плотности 
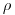среды, через которую проходит γ-излучение:
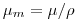(4.9). При помощи массового коэффициента передачи энергии можно рассчитать керму флюенса энергии косвенно ионизирующих частиц:
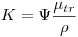(4.10). При равновесии вторичных частиц превращенная энергия в элементе массы равна сумме энергий тормозного излучения всех вторичных заряженных частиц, возникших в этом элементе массы, при их полном поглощении. Согласно формулам (4.8) и (4.10), в случае равновесия вторичных частиц имеем
(4.11). При помощи этого уравнения с учетом выражения (4.4) получаем соотношение, имеющее важное значение в дозиметрии:
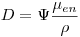(4.12). Уравнение (4.12) является основой для расчета чувствительности равновесных зондов. Поскольку равновесие вторичных частиц на практике никогда полностью не реализуется, то рассчитать поглощенную дозу излучения по этому уравнению можно лишь приближенно. Однако достигаемая точность в большинстве практических случаев достаточна.