3.1.2. Процессы взаимодействия заряженных частиц
При взаимодействии заряженных частиц с атомами вещества важно различать упругие и неупругие столкновения с орбитальными электронами и атомными ядрами, соответственно. Неупругие столкновения с орбитальными электронами приводят к возбуждению атома. Если энергия заряженной частицы достаточно высока, чтобы вырвать орбитальный электрон из атома, происходит ионизация. В этом случае говорят об ионизационных потерях. Если орбитальному электрону передать энергию 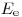 , то энергия заряженной частицы после взаимодействия составит
, то энергия заряженной частицы после взаимодействия составит
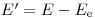 (3.5),
(3.5), где 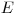 – начальная энергия заряженной частицы. Вероятность того, что переданная электрону энергия лежит в интервале
– начальная энергия заряженной частицы. Вероятность того, что переданная электрону энергия лежит в интервале  , задается дифференциальным сечением (здесь, отнесенным к энергии электрона):
, задается дифференциальным сечением (здесь, отнесенным к энергии электрона):
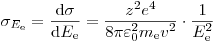 (3.6),
(3.6), которое можно использовать в нерелятивистском приближении. Здесь 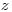 – зарядовое число и
– зарядовое число и 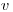 – скорость заряженной частицы,
– скорость заряженной частицы, 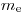 – масса электрона,
– масса электрона, 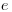 – заряд электрона и
– заряд электрона и 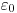 – диэлектрическая проницаемость вакуума. Так как квадрат скорости
– диэлектрическая проницаемость вакуума. Так как квадрат скорости 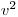 прямо пропорционален энергии
прямо пропорционален энергии 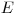 частицы, то вероятность ионизационных эффектов уменьшается с ростом энергии. Пропорциональность
частицы, то вероятность ионизационных эффектов уменьшается с ростом энергии. Пропорциональность 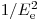 в уравнении (3.6) означает, что более вероятна передача малых энергий. Из дифференциального сечения можно получить величину средних потерь энергии заряженных частиц на единицу пути в веществе с атомным номером
в уравнении (3.6) означает, что более вероятна передача малых энергий. Из дифференциального сечения можно получить величину средних потерь энергии заряженных частиц на единицу пути в веществе с атомным номером 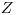 :
:
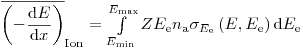 (3.7).
(3.7). Атомная плотность (число атомов в единице объема) находится как
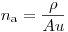 (3.8),
(3.8), где 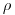 – плотность,
– плотность, 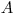 – относительная атомная масса,
– относительная атомная масса, 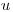 – атомная единица массы. Пределы интегрирования
– атомная единица массы. Пределы интегрирования 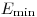 и
и 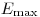 определяются из квантово-механических соображений. Из уравнения (3.7) следует соотношение для ионизационных потерь электронов
определяются из квантово-механических соображений. Из уравнения (3.7) следует соотношение для ионизационных потерь электронов
 (3.9),
(3.9), тогда как для тяжелых заряженных частиц
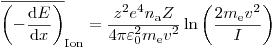 (3.10).
(3.10). Значения средних потенциалов ионизации 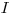 для соответствующих атомов можно найти в справочной литературе. При более высоких энергиях частиц сказывается влияние электрического поля вокруг заряженной частицы, при этом в уравнения 3.9 и 3.10 необходимо вводить релятивистские поправки.
для соответствующих атомов можно найти в справочной литературе. При более высоких энергиях частиц сказывается влияние электрического поля вокруг заряженной частицы, при этом в уравнения 3.9 и 3.10 необходимо вводить релятивистские поправки.
Если заряженная частица влетает в окрестность атомного ядра, то она отклоняется от первоначального направления кулоновским полем. Этот процесс представляет собой неупругое столкновение с ядром, при котором частица теряет энергию, испускаемую в виде фотонного излучения (тормозное излучение). В этом случае имеют место радиационные потери. Интенсивность тормозного излучения описывается формулой
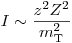 (3.11),
(3.11), где 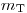 – масса частицы. Радиационные потери не проявляются для тяжелых заряженных частиц (если только они не имеют чрезвычайно высокую энергию), так как
– масса частицы. Радиационные потери не проявляются для тяжелых заряженных частиц (если только они не имеют чрезвычайно высокую энергию), так как 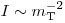 , но для электронов его нужно учитывать в первую очередь. Испускаемое фотонное излучение имеет непрерывный энергетический спектр во всем диапазоне энергий от
, но для электронов его нужно учитывать в первую очередь. Испускаемое фотонное излучение имеет непрерывный энергетический спектр во всем диапазоне энергий от 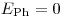 до энергии частицы
до энергии частицы 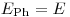 . Дифференциальное сечение взаимодействия, описывающее вероятность того, что энергия фотона лежит в интервале
. Дифференциальное сечение взаимодействия, описывающее вероятность того, что энергия фотона лежит в интервале 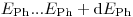 , определяется как
, определяется как
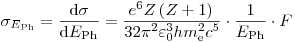 (3.12),
(3.12), где  – постоянная Планка,
– постоянная Планка, 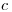 – скорость света,
– скорость света, 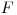 – слабо меняющаяся функция от
– слабо меняющаяся функция от 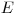 и
и 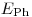 . Средние потери энергии заряженных частиц на единице пути находятся как
. Средние потери энергии заряженных частиц на единице пути находятся как
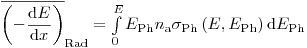 (3.13).
(3.13). Интегрирование дает
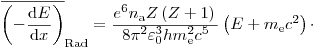 (3.14)
(3.14) 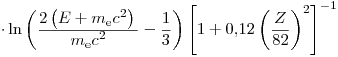
Уравнение (3.14) справедливо, если  , в этом случае экранированием поля ядра полем орбитальных электронов можно пренебречь. Особым видом тормозного излучения является сплошной рентгеновский спектр, возникающий при торможении ускоренных электронов на аноде рентгеновской трубки (см. раздел 2.5).
, в этом случае экранированием поля ядра полем орбитальных электронов можно пренебречь. Особым видом тормозного излучения является сплошной рентгеновский спектр, возникающий при торможении ускоренных электронов на аноде рентгеновской трубки (см. раздел 2.5).
При взаимодействии заряженных частиц с веществом ионизационные и радиационные эффекты проявляются одновременно. Ниже критической энергии 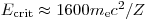 доминируют ионизационные потери, выше
доминируют ионизационные потери, выше 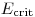 – радиационные. Для воздуха
– радиационные. Для воздуха 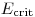 составляет примерно 100 МэВ, для алюминия – около 60 МэВ, для свинца – около 10 МэВ.
составляет примерно 100 МэВ, для алюминия – около 60 МэВ, для свинца – около 10 МэВ.
Если заряженная частица рассеивается на атомном ядре без испускания фотонного излучения, говорят об упругом столкновении. Дифференциальное сечение этого процесса, называемого Резерфордовским рассеянием, равно
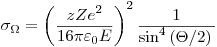 (3.15),
(3.15), где 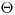 – угол рассеяния. Из уравнения (3.15) видно, что Резерфордовское рассеяние преобладает для малых углов и небольших энергий частиц, например, в конце пути частицы после значительного снижения энергии за счет ионизационных эффектов.
– угол рассеяния. Из уравнения (3.15) видно, что Резерфордовское рассеяние преобладает для малых углов и небольших энергий частиц, например, в конце пути частицы после значительного снижения энергии за счет ионизационных эффектов.
Упругие столкновения заряженных частиц с орбитальными электронами не приводят к существенным потерям энергии, и поэтому не представляют интерес в контексте физики радиационной защиты.