7.5. Обработка результатов эксперимента

При проведении работ с использованием радиоактивных индикаторов следует иметь в виду, что систематические и случайные погрешности, возникающие на различных этапах эксперимента, могут значительно превышать как погрешности, обусловленные статистическим характером распада, так и суммарные погрешности радиометрических определений. Возможны также погрешности, которые в экспериментах, проводимых в строго одинаковых условиях, выступают как систематические, а при варьировании условий эксперимента — как случайные. Объективная оценка точности и надежности получаемых данных может быть найдена только в результате повторения всего эксперимента в несколько различающихся условиях (например, при определении растворимости следует варьировать время контакта осадка с раствором, условия разделения фаз, величину удельной активности исходного меченого соединения и т. п.). На основании результатов параллельных экспериментов рассчитывают среднее и дисперсию и находят погрешность среднего арифметического при заданной доверительной вероятности. Если параллельные опыты выполняются в одних и тех же условиях, то нужно иметь в виду, что получаемая на основании этих данных опенка точности будет характеризовать лишь минимальный уровень рассеяния значений определяемой величины.

В тех случаях, когда невозможно повторение всего эксперимента от начала до конца, выполняют параллельные определения на отдельных этапах работы и оценивают точность окончательного результата с помощью закона накопления погрешностей. При этом погрешность результата косвенных измерений также может оказаться заниженной, если не были учтены какие-либо источники рассеяния. Тем не менее, оценка погрешности результата на основании закона накопления погрешностей бывает очень полезна, так как позволяет выявить те экспериментальные операции, которые приводят к наиболее значительному рассеянию результатов.

Чтобы снизить погрешность результата косвенных измерений, при выполнении этих операций следует увеличивать число параллельных либо добиться уменьшения погрешностей отдельного измерения путем усовершенствования методики работы. Закон накопления погрешностей целесообразно использовать и на стадии планирования эксперимента, когда предстоит выбрать методику, которая давала бы наиболее точные результаты.

Когда определяющими являются погрешности радиометрических определений, важно выяснить, отсутствуют ли погрешности, не связанные со статистическим характером радиоактивного распада. Такие погрешности могут возникать на самых различных этапах экспериментальной работы; они нарушают пуассоновский характер распределения результатов измерения радиоактивности. Поэтому обязательно проверяют, можно ли считать, что результаты измерения активности распределены по закону Пуассона. Последовательность операций при измерениях может различаться в зависимости от условий проведения эксперимента. Опишем две наиболее характерные ситуации.

Ситуация 1. Измеряется серия препаратов, приготовленных одним и тем же способом на разных стадиях эксперимента или в различных экспериментах. Для проверки гипотезы о пуассоновском характере распределения результатов измерений радиоактивности проводят ~10 измерений скорости счета (вместе с фоном) одного из препаратов, каждый раз поворачивая его на некоторый случайный угол. Если с помощью χ²-критерия показано, что нет оснований отвергнуть предположение о распределении результатов в соответствии с законом Пуассона, то для остальных препаратов рассчитывают оптимальную продолжительность измерений, необходимую для того, чтобы при доверительной вероятности 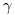относительная флуктуация 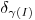не превышала заданной величины. Можно поступить иначе – приготовить препарат с такой скоростью счета, чтобы при фиксированном времени измерения была достигнута требуемая точность регистрации. Скорость счета препарата находят, задаваясь величиной фона, временем измерения и относительной флуктуацией скорости счета при доверительной вероятности , :

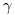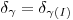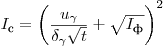(7.55).

Выполнив измерения регистрируемой активности в течение требуемого времени, рассчитывают погрешности средних значений скоростей счета при доверительной вероятности 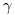. Если единственным источником рассеяния является статистический характер радиоактивного распада, то погрешности равны

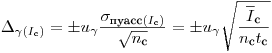(7.56);

;

,

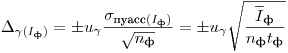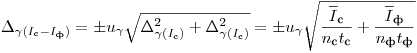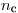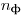где и — число измерений препарата с фоном и фона. Если 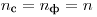, то

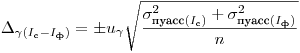(7.57).

В тех случаях, когда использование критерия 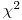показывает, что эмпирическое распределение результатов измерения радиоактивности существенно отличается от распределения Пуассона, нет смысла находить оптимальную продолжительность измерений или готовить препарат с заданной скоростью счета. Достаточно провести несколько (чем больше, тем лучше) измерений каждого препарата и фона продолжительностью по 1 мин. Естественно, что для того препарата, который использовали при проверке пуассоновского характера распределения результатов, дальнейшие измерения проводить не нужно, поскольку для него уже получена достаточно большая выборочная совокупность значений .

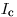Если присутствуют погрешности, не связанные со статистическим характером распада, то погрешность результата оценивают с помощью t-распределения на основании выборочного среднего квадратического отклонения :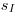

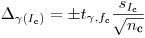(7.58);

,

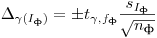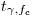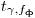где и —доверительные границы распределения Стьюдента при доверительной вероятности 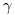и числе степеней свободы 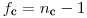и .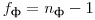

Погрешность скорости счета препарата за вычетом фона, соответствующую доверительной вероятности 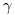, рассчитывают по формуле

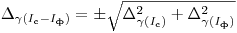(7.59).

Если число измерений препарата с фоном и фона одинаково,

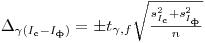(7.60).

На схеме 1 показана последовательность операций при выполнении радиометрических определений в разобранном случае. Рассмотрим другую ситуацию.

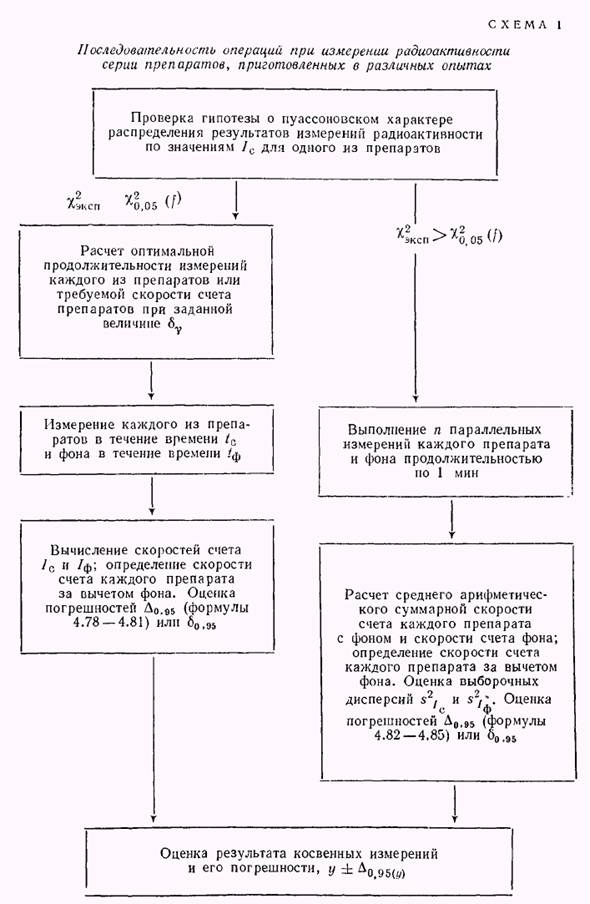
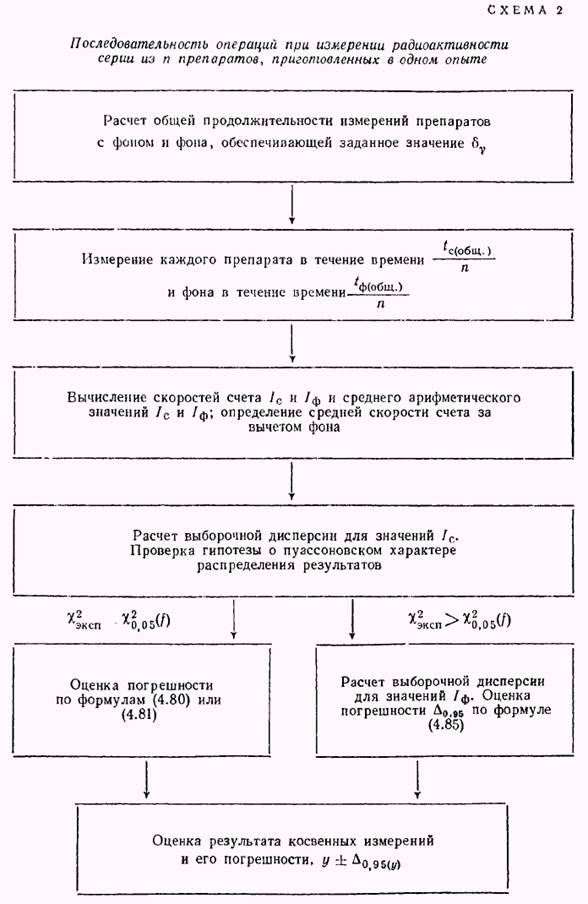
Ситуация 2. Измеряется серия препаратов, приготовленных в одном и том же опыте. Пусть все препараты приготовлены одним и тем же способом из одинаковых объемов радиоактивного раствора (заметим, что число параллельных препаратов 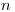должно быть не менее 3). Тогда поступают следующим образом. Рассчитывают оптимальную общую продолжительность измерени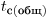й и 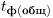при которой обеспечивается требуемое значение относительной флуктуации результата (средней скорости счета препаратов за вычетом фона) 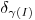. Проводят измерение регистрируемой активности каждого препарата в течение времен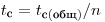и и 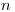измерений фона продолжительностью 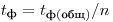каждое. С помощью χ²-критерия проверяют, можно ли считать, что значения 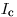распределены в соответствии с законом Пуассона.

Если нет оснований отвергнуть предположение о том, что эмпирическое распределение соответствует пуассоновскому, то оценивают погрешность результата измерений по формулам (7.56) или (7.57). В противном случае для расчета погрешности используют формулу (7.60). На заключительном этапе обработки данных оценивают погрешность результата косвенных измерений. Описанная последовательность операций показана на схеме 2. Следует иметь в виду, что если препараты готовились из различных объемов радиоактивного раствора или были измерены в различных условиях (разные подложки, геометрические коэффициенты и т. п.), то проверить гипотезу о пуассоновском характере распределения результатов нельзя. В этом случае пересчитывают все результаты к одинаковому объему раствора или одинаковым условиям измерения и оценивают погрешность по формулам (7.58) – (7.60).