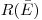3.6. Измерение активности толстослойного источника бета-излучения

В ряде случаев данный метод может быть использован как абсолютный метод измерения удельной активности радионуклидов (при условии учета всех поправок).

Общие сведения. При радиометрических измерениях или исследованиях, связанных с применением радиоактивных индикаторов возникает необходимость определить их удельную активность в веществе.

Удельная активность определяется по отношению общей активности образца к его массе. Обычно ее выражают в Бк/кг. Определить удельную активность можно, измерив абсолютную активность пробы и ее массу:

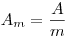(3.133).

Однако в ряде случаев удельную активность проб целесообразнее определять по измерению β-излучения толстослойного источника. Измерения основаны на том, что выход β -частиц с поверхности толстослойного источника, т.е. число β-частиц, вылетающих с единичной поверхности толстослойного источника в единицу времени пропорционален не полной, а удельной активности и не изменяется с увеличением его толщины. Под толстослойным подразумевается источник, толщина которого больше пробега β-частиц, в материале источника.

Если скорость счета установки при измерении удельной активности толстослойного препарата равна 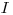, то его удельная активность 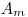может быть определена по соотношению:

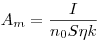(3.134),

где 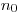— выход β-частиц с поверхности источника, имеющего единичную удельную активность;

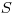— поверхность источника, см;

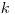— поправка на поглощение и рассеяние β -излучения на пути от поверхности источника до чувствительного объема счетчика ;

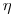— доля β -частиц, летящих в направлении окна торцевого счетчика, от общего числа вылетающих в телесный угол 4π- поправка на геометрию измерения.

Рассмотрим способы определения величин, входящих в уравнение (3.134).

Если связать выход β-частиц с поверхности толстослойного источника 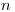с пробегом β-частиц в веществе 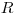, коэффициентом обратного рассеяния 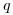и удельной активностью 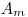, то будет иметь месте следующее соотношение:

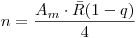(3.135),

где 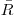— средний путь β -частиц данного радионуклида в материале источника, определяемый по уравнению:

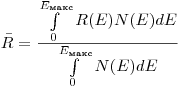(3.136),

где 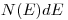-энергетическое распределение β -спектра;

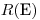— пробег электронов с энергией Е.

Для приближенных вычислений выхода β -частиц с поверхности толстослойного источника среднюю длину пути можно заменить величиной пробега частиц энергии :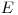

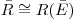(3.137).

Таблица 3.16

Средние пути β-частиц радионуклидов в различных химических элементах, г/см²

В большинстве случаев материал источника представляет собой сложное вещество. Обозначим через 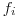весовую долю атомов i-го простого вещества в сложном, а через 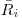— среднюю длину пути β-частиц в i-м простом веществе. Тогда величину 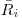в сложном веществе можно найти из уравнения:

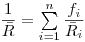(3.138).

Коэффициент обратного рассеяния β-излучения (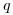) зависит от атомного номера вещества (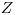), возрастая с увеличением 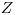(рис.3.40).

Рис. 3.40. Зависимость коэффициента обратного рассеяния β-излучения (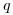 от атомного номера 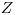вещества)

Если известны коэффициенты обратного рассеяния для простых веществ, входящих в состав сложного, то величину 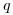для сложного вещества можно определить из следующего соотношения:

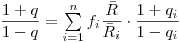(3.139),

где 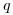и 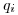— коэффициенты обратного рассеяния в сложном и простом веществах соответственно, 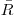и 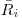— пробег электронов данной энергии 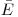в сложном и простом веществах.

Соотношение (3.139) дает хорошее совпадение с экспериментально полученными величинами.

Таким образом, и величина коэффициента обратного рассеяния β-излучения 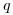, и средний путь β-частиц в веществе источника увеличивается с ростом атомного номера 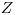материала источника. В целом же выход β-излучения (см. рис. 3.41) с поверхности толстослойного источника слабо зависит от величины .

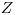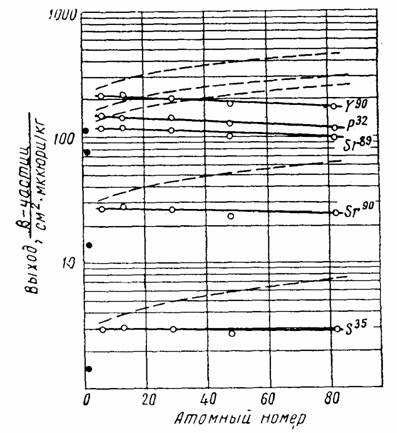
Рис. 3.41. Зависимость выхода β-частиц с поверхности толстослойного источника от атомного номера вещества

Если в состав вещества толстослойного источника входят главным образом элементы, имеющие атомный номер 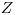< 30, для которых выход β-частиц мало изменяется с изменением 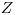, то для таких проб величину 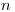можно определить по формуле:

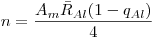(3.140).

Для алюминия 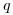= 0,26, поэтому, учитывая соотношение (5) и размерности величин, для выхода β-частиц можно записать следующее уравнение:

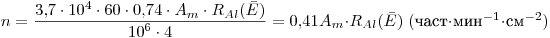(3.141),

где 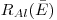— максимальный пробег β-частиц средней энергии 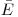в алюминии, мг/см², 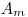— удельная активность, мкКи/кг.

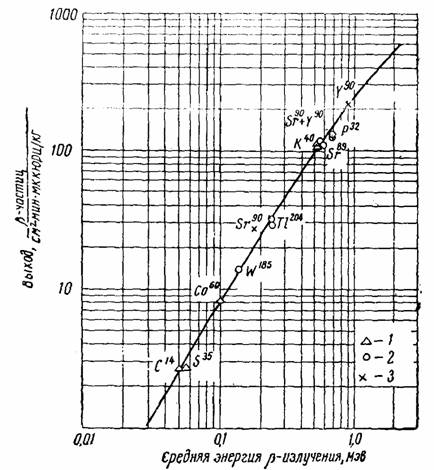
Рис. 3.42. Зависимость выхода β-частиц с поверхности толстослойного источника от средней энергии β-излучения

Проверка показала, что отклонение экспериментальных точек от кривой на рис. 3.42 не превышает 20% для всех источников, атомный номер материала которых меньше 30. Таким образом, если не требуется большой точности измерения, можно пользоваться величиной выхода, рассчитанной по формуле (3.141) при любом составе источника.

При измерении методом толстой пробы необходимо учитывать, что для толстослойного источника может иметь место не изотропный характер вылета частиц с его поверхности. Данный факт необходимо учитывать внесением поправок в расчет относительного телесного угла 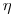или использовать геометрию измерений, близкую к 2π.