12.7. Использование амбиентного эквивалента дозы для оценки эффективных доз облучения

В соответствии с рекомендациями Комиссии МКРЗ сами пределы эквивалентной дозы, или вторичные пределы, могут быть использованы для определения производных пределов, таких, как мощность эквивалентной дозы на рабочем месте. Эта возможность используется здесь с некоторым подчеркиванием связи между нормируемым параметром (эффективная или эквивалентная) доза и значениями поддающейся физическому определению величине .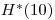

В табл. 12.3 показаны отношения эффективной эквивалентной дозы к эквивалентной дозе в оболочке для фотонов и нейтронов, падающих на соответствующие фантомы в плоскопараллельных пучках. Пригодность величины 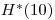для целей радиационной безопасности определяется близостью отношения к единице или менее единицы. Благодаря этим критериям эквивалентная доза в оболочке обычно используется для фотонов и нейтронов даже в том случае, если необходима осторожность в определенных энергетических интервалах.

Скудная информация по электронам указывает на то, что отношение составляет меньше единицы для схем ПЗ и ЗП при использовании плоскопараллельных пучков в области энергий приблизительно от 5 до 20 МэВ.

В том случае, если значения индекса должны быть основой производных величин, то связь между ними должна быть реалистичной в том смысле, что производная величина должна близко соответствовать вторичной величине или быть осторожным отражением ее.

Исследования данных для фотонов и нейтронов демонстрируют тот факт, что это верно для эквивалентной дозы в оболочке относительно глубинной эквивалентной дозы для обоих излучений в случае плоскопараллельных пучков и изотропного облучения, с некоторыми оговорками в отношении низких энергий нейтронов. Вычисления для электронов из ограниченных данных, упомянутых в основном тексте, указывают на то, что отношение близко к единице или немного превышает ее для мононаправленных пучков при энергиях приблизительно от 5 до 20 МэВ.

Тот факт, что амбиентный эквивалент дозы позволяет достаточно адекватно оценить величину эффективной дозы в полях внешнего излучения, независимо от энергии падающих частиц, привело к тому, что сейчас почти все дозиметрические приборы (за рубежом) градуируются именно в этой величине.

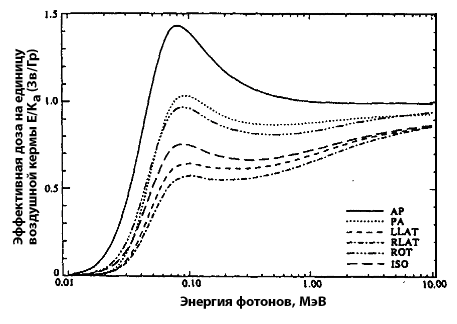
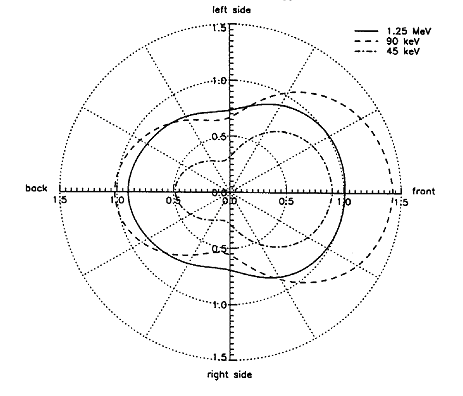
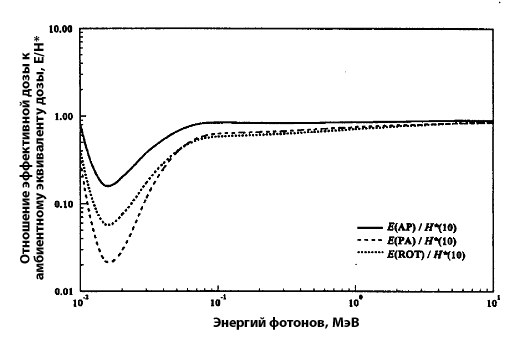
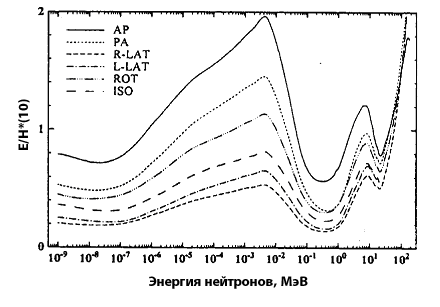
Наиболее современные данные (Публикация МКРЗ 74) по зависимости эффективной дозы от энергетического и углового распределения падающего фотонного излучения приведены на рис. 12.2 и 12.3.

Таблица 12.3

Отношение эффективной эквивалентной дозы 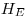к амбиентному эквиваленту дозы 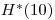для фотонов и нейтронов, падающих на антропоморфный фантом и на сферу МКРЕ в плоскопараллельном пучке

Энергия, МэВ	Фотоны,	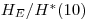	Нейтроны,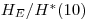
	ПЗ	ЗП	ПЗ	ЗП
2,5 E-08			(0,50)	(0,33)
1,0 E-07			(0,42)	(0,26)
1,0 E-06			0,43	0,25
1,0 E-05			0,48	0,30
1,0 E-04			0,58	0,37
1,0 E-03			0,62	0,40
1,0 E-02	0,81	0,00	0,53	0,30
1,5 E-02	0,19	0,04
2,0 E-02	0,24	0,09	0,40	0,19
3,0 E-02	0,42	0,21
4,0 E-02	0,59	0,36
5,0 E-02	0,73	0,49	0,31	0,10
6,0 E-02	0,79	0,57
8,0 E-02	0,85	0,65
1,0 E-01	0,87	0,68	0,29	0,08
1,5 E-01	0,87	0,70
2,0 E-01	0,87	0,72	0,31	0,07
3,0 E-01	0,86	0,72
4,0 E-01	0,87	0,74
5,0 E-01	0,88	0,76	0,34	0,12
6,0 E-01	0,88	0,78
8,0 E-01	0,89	0,80
1,0 E+00	0,90	0,82	0,42	0,16
1,5 E+00	0,90	0,84	0,51	0,24
2,0 E+00	0,90	0,85	0,61	0,34
3,0 E+00	0,92	0,87	0,69	0,46
4,0 E+00	0,94	0,90	0,73	0,53
5,0 E+00	0,95	0,92	0,87	0,65
6,0 E+00	0,96	0,93	0,91	0,69
8,0 E+00	0,98	0,95	0,91	0,71
1,0 E+01	0,98	0,96	0,92	0,72
1,4 E+01			(0,92)	(0,80)

Примечание: Хотя в табл. 12.3. приведены отношения 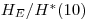, но аналогичные результаты будут наблюдаться и для отношения 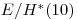, что проиллюстрировано на рис. 12.4 — 12.5.

Рис. 12.2 — 12.3. Отношение эффективной дозы к воздушной керме (Зв/Гр) для различных условий облучения фотонами

Рис. 12.4 — 12.5. Отношение эффективной дозы к амбиентному эквиваленту дозы для различных условий облучения фотонами и нейтронами

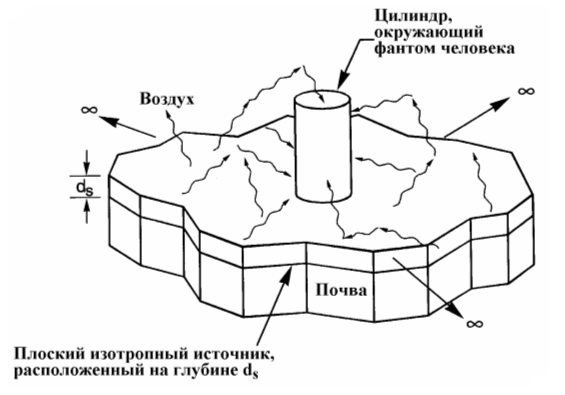
Рассмотренные выше методы оценки доз облучения человека применимы в том случае, когда мы достаточно точно знаем спектр излучения падающего на тело человека в определенной геометрии. Тем не менее, серьезный практический интерес представляет другая ситуация — случай, когда достаточно точно известен радионуклидный состав излучателей и их геометрия. Эта ситуация достаточно типична для случаев облучения человека от радионуклидов, рассеянных в окружающей среде (облучение от радиоактивного облака, поверхности почвы, загрязненной радионуклидами с различными уровнями заглубления и т.д.). При этом необходимо учитывать как пространственно-угловое распределение падающих на человека (или антропоморфный фантом) гамма-квантов, так и их энергетическое распределение, обусловленное рассеянием излучения в окружающей среде и теле человека.

Данный процесс может быть описан уравнением Больцмана, описывающем перенос незаряженных частиц:

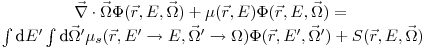(12.1),

где 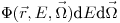— угловой флюенс частиц с энергией от 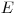до 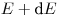, движущихся в точке 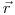в телесном угле от 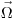до 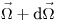; 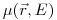— коэффициент линейного ослабления для частиц с энергией 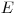в точке 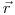; 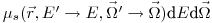— вероятность на единицу пробега того, что частица с начальной энергией 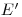и направлением движения 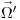будет в точке 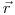претерпевать рассеяние с энергией от 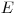до 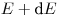в телесном угле от 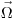до 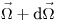; 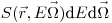— число частиц источника с энергией от 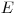до 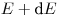, испущенных в точке 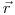в телесном угле от 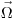до .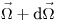

Уравнение (12.1) может быть записано в операторной форме

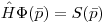(12.2),

где 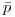описывает фазовое пространство координат, энергии и направления движения частиц. После того, как получено уравнение (12.2), то доза в органе может быть вычислена из уравнения

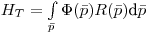(12.3),

где 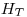— доза в органе; 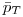— фазовое пространство ткани или органа 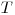; 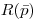— функция отклика, т.е. вклад в формирование дозы 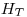единичного углового флюенса.

В принципе, уравнения (12.2) и (12.3) могут быть впрямую решены методом Монте-Карло. Однако такое решение не всегда удобно, т.к. оно сочетает в себе расчет переноса излучения на больших пространствах в окружающей среде и в относительно малых объемах антропоморфного фантома. На практике эта задача решается в два этапа:

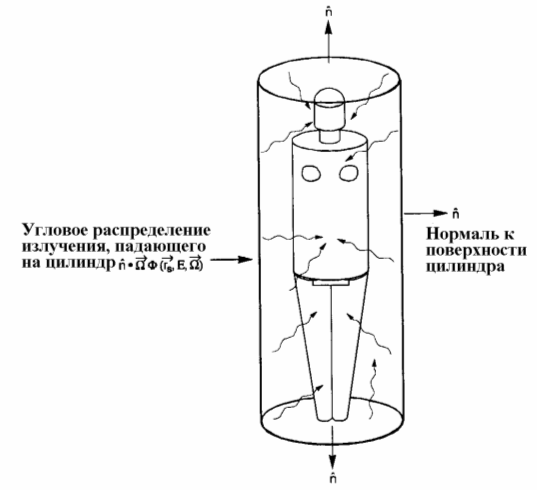
• На первом этапе рассчитывается поле излучения, падающее на цилиндрическую поверхность, окружающую антропоморфный фантом (рис. 12.6);
• На втором этапе расчетов производится расчет эквивалентных доз на внутренние органы, обусловленных излучением цилиндрического поверхностного источника, окружающего фантом (рис. 12.7).

Рис. 12.6. Расчет поля излучения, падающего на цилиндрическую поверхность, окружающую антропоморфный фантом

Рис. 12.7. Расчет эквивалентных доз на внутренние органы, обусловленных излучением цилиндрического поверхностного источника, окружающего фантом