11.1.1. Базовые величины

Исходные коэффициенты риска
Основные модели экстраполяции

Существует два основных вида коэффициентов риска: половозрастные коэффициенты смертности 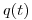и заболеваемости 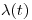. Эти коэффициенты определяются, как плотность условной вероятности смерти (заболеваемости) в возрасте .

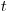Пусть 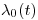— онкологическая заболеваемость в определенном возрасте 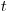от всех причин, в конкретной необлученной популяции (базовая частота). Тогда заболеваемость с учетом облучения будет выражаться следующим образом:

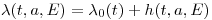(11.1),

где 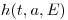— избыточная заболеваемость в определенном возрасте 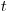, связанная с облучением дозой 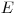в возрасте 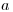(заметим, что 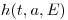= 0 для < ).

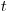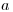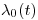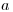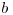Общий вид заболеваемости может быть представлена в первом приближении зависимостью , где коэффициенты , и 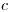равны:

Тип заболевания	Пол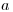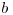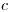
Лейкемия	Мужской	4,4·10-10	3,00	15·10-6
	Женский	3,0·10-10	2,90	15·10-6
Злокачественные опухоли	Мужской	3,0·10-10	5,14	15·10-6
	Женский	3,9·10-10	4,90	15·10-6

Наибольшую трудность в оценке радиационного риска вызывает определение избыточной смертности и заболеваемости, вызванной облучением. Прежде всего, это вызвано ограниченностью информации о биологическом механизме радиационного канцерогенеза.

Необходимую информацию о вероятности заболеваемости радиационно-индуцированным раком получают, обследуя группы людей, подвергшихся воздействию ионизирующего излучения. Самой большой такой группой является когорта, состоящая из более 90 000 лиц, переживших атомные бомбардировки в Японии.

Обычно период наблюдения за выборкой облученной группы людей соответствует некоторому времени, которое меньше времени жизни. Тогда необходима экстраполяция оценки вероятности инициации рака, чтобы получить риск заболеваемости радиационно-индуцированным раком за полное время жизни. Существуют две основные модели экстраполяции риска:

1. модель абсолютного риска (аддитивная);
2. модель относительного риска (мультипликативная).

Согласно первой моделидополнительная частота возникновения радиационно-индуцированного рака не зависит от базовой (спонтанной) частоты заболевания. В соответствии со второй моделью облучение вызывает увеличение вероятности заболевания, пропорциональное базовой частоте.

Следует учитывать, что риск онкологической заболеваемости проявляется после некоторого латентного периода 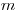, равный 2 года для лейкемии, 5 лет для рака щитовидной железы и 10 лет для остальных онкологических заболеваний.

В простой аддитивной модели 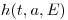не изменяется для 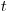> 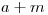и имеет следующий вид:

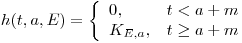(11.2),

В простой мультипликативной модели 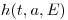меняется с изменением 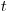, как постоянное кратное базовой частоте конкретного рака у необлученной популяции:

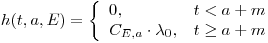(11.3).

Примерный вид зависимостей (реальной и «идеальной») представлен на рис. 11.1. Протяженность плато 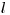составляет 40 лет в случае лейкемии, а для остальных видов онкозаболеваний равна .

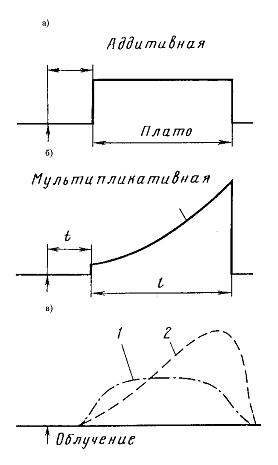
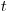Рис. 11.1. Иллюстрация двух простых моделей экстраполяции. Кривые а, б — соответсвуют идеальной реализации моделей; в — реальные зависимости; — минимальный латентный период; 1 — вероятная реальная форма кривой для аддитивной модели; 2 — вероятная реальная форма кривой для мультипликативной модели.

Функция дожития

Функция дожития определяется как вероятность достижения человеком возраста 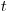(с рождения).

В отсутствии облучения вероятность дожития до возраста 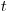(с рождения) задается функцией 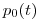и может быть вычислена по формуле:

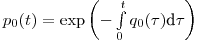(11.4),

где 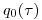— смертность в определенном возрасте 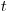от всех причин, в конкретной необлученной популяции.

С учетом ожидаемого сокращения продолжительности жизни в связи с заболеванием радиационно-индуцированным раком, вызванным облучением человекаэффективной дозой 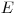в возрасте 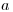, вероятность дожития (с рождения) до возраста 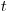определяется по формуле:

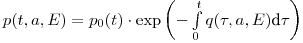(11.5),

где 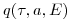— избыточная смертность в определенном возрасте 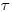, связанная с облучением дозой 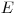в возрасте 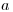( 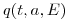= 0 для < ).

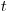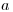Следует отметить, что

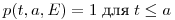(11.6).

(облучение в возрасте 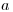предполагает дожитие до этого возраста).

Связь радиационно-индуцированной заболеваемости 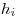и обусловленной ею смертностью 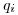может быть выражена как

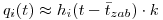(11.7),

где 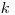— летальность онкологического заболевания данной локализации; 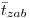— средний период между возникновением заболевания и летальным исходом.

Более строго эта зависимость может быть выражена как

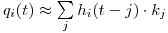(11.8),

где 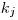— доля заболевших с продолжительностью интервала от между заболеванием и смертью, равному 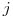лет.

Для человека возраста 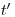вероятность достижения возраста 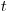равна:

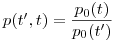(11.9).

По аналогии может быть найдена функция дожития 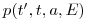— вероятность человека возраста 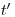достигнуть возраста 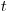, при облучении дозой 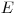в возрасте :

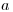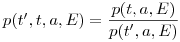(11.10).

Ожидаемая продолжительность жизни

Полная ожидаемая продолжительность жизни 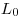(с рождения) равна:

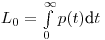(11.11).

Для человека возраста 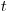ожидаемая продолжительность оставшейся жизни 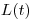определяется по формуле:

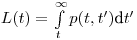(11.12).

Отметим, что

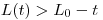(11.13).